Clase 2: Algoritmos de Valores propios¶

Bibliografía de la Clase:

Numerical Linear Algebra.L.N. Trefethen. Chapter 5: Lecture 25 Overview of Eigenvalue Algorithms
Introduction to Linear Algebra. Gilbert Strang. Chapter 6 Eigenvalues and Eigenvectors
Guía profesor Luis Salinas

Alternativa 1: Polinomio característico¶

La primera idea para el cálculo de los valores y vectores propios de una matriz 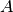$A$ es encontrar su polinomio característico, cuyas raíces son los valores propios, para luego proceder a encontrar sus respectivos vectores propios.

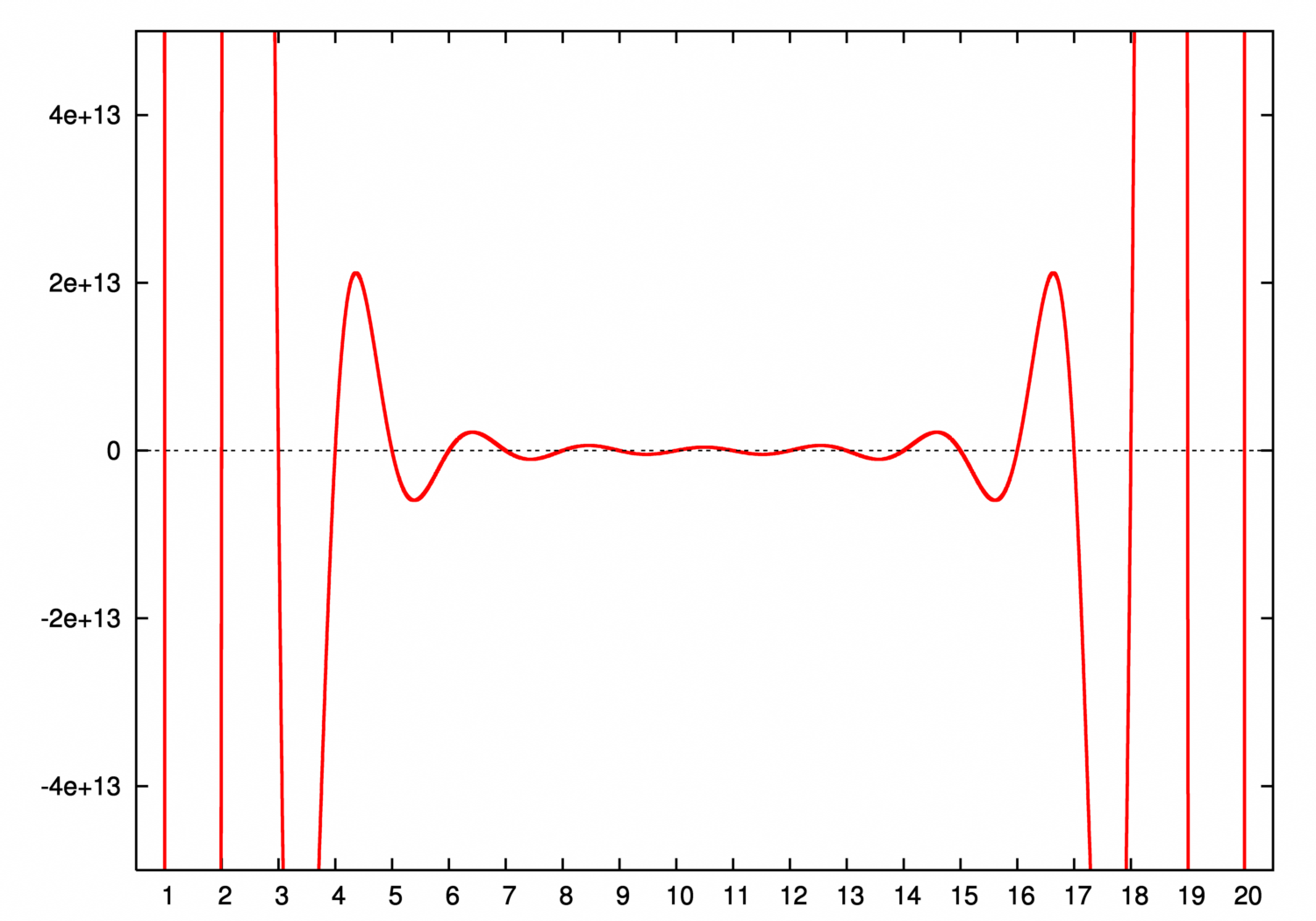
La imagen mostrada corresponde a el polinomio cuyas raíces son $\lambda_i=i , \quad \forall i=1:20$ . Se ve claramente que es un problema mal condicionado, debido a que el polinomio encontrado es muy sensible a sus coeficientes.

Es decir, hemos transformado un problema bien condicionado, en uno mal condicionado.

Problema

La búsqueda de raíces en un polinomio, es un problema mal condicionado (ver Clase Condicionamiento CC1). Por otro lado, se sabe del Algebra que no existe una fórmula para determinar los ceros de un polinomio arbitrario de grado 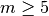$m \geq 5$ a partir de sus coeficientes.

Lo anterior muestra que no es posible expresar las raíces de un polinomio como una expresión algebraica y por lo tanto la única forma de obtenerlos es de forma iterativa (con un número infinito de pasos).

Nota

La fórmula para resolver ecuaciones de segundo grado ya era conocida por los antiguos babilonios. Fibonacci a principios del siglo XIII encontró solución a la ecuación de tercer grado 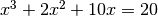$x^3 + 2x^2 +10x =20$ y Scipione del Ferro, Niccolò Tartaglia y Gerolamo Cardano generalizaron la formulación. Ludovico Ferrari, discípulo de Cardano en el siglo XVI expresó la solución para ecuaciones de cuarto grado.

Alternativa 2: Método de Iteración de Potencia¶

Este método consiste en construir una secuencia que converge al vector propio 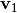$\mathbf{v}_1$ que corresponde al mayor valor propio en valor absoluto 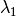$\lambda_1$ . La secuencia es la siguiente:

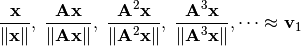
$\frac{\mathbf{x}}{\|\mathbf{x}\|}, \; \frac{\mathbf{Ax}}{\|\mathbf{Ax}\|}, \; \frac{\mathbf{A}^2\mathbf{x}}{\|\mathbf{A}^2\mathbf{x}\|}, \; \frac{\mathbf{A}^3\mathbf{x}}{\|\mathbf{A}^3\mathbf{x}\|}, \dots \approx \mathbf{v}_1$

¿Porqué funciona?

Si escribimos 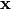$\mathbf{x}$ como una combinación lineal de los vectores propios se tiene:

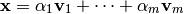
$\mathbf{x} = \alpha_1 \mathbf{v}_1 + \dots + \alpha_m \mathbf{v}_m$

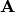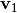Al multiplicar sucesivamente por $\mathbf{A}$ se tiene que el vector propio $\mathbf{v}_1$ es el que predomina la sucesión y por lo tanto la sucesión converge a él:

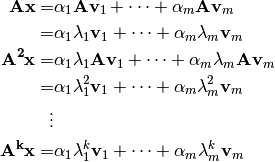
$\mathbf{A} \mathbf{x} =& \alpha_1 \mathbf{A} \mathbf{v}_1 + \dots + \alpha_m \mathbf{A} \mathbf{v}_m \\ =& \alpha_1 \lambda_1 \mathbf{v}_1 + \dots + \alpha_m \lambda_m \mathbf{v}_m \\ \mathbf{A^2} \mathbf{x} =& \alpha_1 \lambda_1 \mathbf{A} \mathbf{v}_1 + \dots + \alpha_m \lambda_m \mathbf{A} \mathbf{v}_m \\ =& \alpha_1 \lambda_1^2 \mathbf{v}_1 + \dots + \alpha_m \lambda_m^2 \mathbf{v}_m \\ \vdots \\ \mathbf{A^k} \mathbf{x} =& \alpha_1 \lambda_1^k \mathbf{v}_1 + \dots + \alpha_m \lambda_m^k \mathbf{v}_m$

Problemas

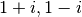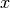El método es muy lento y presenta problemas cuando hay más de un valor propio con módulo máximo (ej: números complejos $1+i,1-i$ ). Hay problemas también si se elige un vector de partida $x$ que no sea combinación lineal del vector $v_1$ .

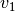Otras Alternativas¶

Los mejores algoritmos para valores propios están basados en un principio distinto: calcular factorizaciones de A que revelen sus factores propios.

Una de las factorizaciones que revelan valores propios (ver Clase 1 ) es llamada la Descomposición de Schur, que existe para toda matriz y permite encontrar una triangularización unitaria.

La estrategia para construir estas factorizaciones consiste en aplicar una secuencia de transformaciones a 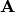$\mathbf{A}$ para introducir ceros donde se requiera.

Descomposición de Schur¶

La descomposición de Schur de una matriz 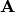$\mathbf{A}$ tiene la siguiente definición:

Factorización de Schur

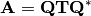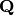$\mathbf{A}=\mathbf{QTQ}^*$ donde $\mathbf{Q}$ es unitaria y 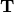$\mathbf{T}$ es una matriz triangular superior.

Teorema¶

Toda matriz 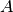$A$ tiene una descomposición de Schur, incluso las matrices deficientes.

Demostración¶

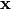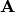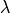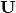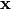Digamos que $\mathbf{x}$ es un vector propio cualquiera de la matriz $\mathbf{A}$ con $\lambda$ como su correspondiente valor propio. Definir la matriz unitaria $\mathbf{U}$ tenga como primera columna el vector $\mathbf{x}$ .

$\mathbf{U} = \left[ \begin{array}{c|c|c|c} \, & \, & \, & \, \\ \, & \, & \, & \, \\ x & u_2 & \cdots & u_m \\ \, & \, & \, & \, \\ \, & \, & \, & \, \end{array} \right]$

Si ahora construimos 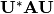$\mathbf{U}^* \mathbf{A} \mathbf{U}$ se tiene:

$\mathbf{U}^* \mathbf{A} \mathbf{U} = \left[ \begin{array}{ccc} \, & \mathbf{x}^* & \, \\ \hline \, & \mathbf{u}_2^* & \, \\ \hline \, & \vdots & \, \\ \hline \, & \mathbf{u}_m^* & \, \end{array} \right] \left[ \begin{array}{c|c|c} \, & \, & \, \\ \, & \, & \, \\ a_1 & \cdots & a_m \\ \, & \, & \, \\ \, & \, & \, \end{array} \right] \left[ \begin{array}{c|c|c|c} \, & \, & \, & \, \\ \, & \, & \, & \, \\ x & u_2 & \cdots & u_m \\ \, & \, & \, & \, \\ \, & \, & \, & \, \end{array} \right]$

Al multiplicar se tiene:

$\mathbf{U}^* \mathbf{A} \mathbf{U} = \left[ \begin{array}{c|ccc} \lambda & x^*.A.u_2 & \dots & x^*.A.u_m \\ \hline 0 & u_2^*.A.u_2 & \dots & u_2^*.A.u_m \\ \vdots & \vdots & & \vdots \\ 0 & u_m^*.A.u_2 & \dots & u_m^*.A.u_m \end{array} \right] = \left[ \begin{array}{c|c} \lambda & \mathbf{B} \\ \hline \mathbf{0} & \mathbf{C} \end{array} \right]$

Por hipótesis inductiva, la matriz 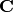$\mathbf{C}$ también tiene descomposición de Schur, por lo tanto:

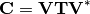
$\mathbf{C} = \mathbf{V} \mathbf{T} \mathbf{V}^*$

Entonces, como:

$\mathbf{U}^* \mathbf{A} \mathbf{U} =& \left[ \begin{array}{c|c} \lambda & \mathbf{B} \\ \hline \mathbf{0} & \mathbf{C} \end{array} \right] \\ =& \left[ \begin{array}{c|c} \lambda & \mathbf{B} \\ \hline \mathbf{0} & \mathbf{V} \mathbf{T} \mathbf{V}^* \end{array} \right] =& \left[ \begin{array}{c|c} 1 & \mathbf{0} \\ \hline \mathbf{0} & \mathbf{V} \end{array} \right] \left[ \begin{array}{c|c} \lambda & \mathbf{BV} \\ \hline \mathbf{0} & \mathbf{T} \end{array} \right] \left[ \begin{array}{c|c} 1 & \mathbf{0} \\ \hline \mathbf{0} & \mathbf{V}^* \end{array} \right] \\$

equivalentemente se tiene que:

$\left[ \begin{array}{c|c} 1 & \mathbf{0} \\ \hline \mathbf{0} & \mathbf{V}^* \end{array} \right] \mathbf{U}^* \mathbf{A} \mathbf{U} \left[ \begin{array}{c|c} 1 & \mathbf{0} \\ \hline \mathbf{0} & \mathbf{V} \end{array} \right] =\left[ \begin{array}{c|c} \lambda & \mathbf{BV} \\ \hline \mathbf{0} & \mathbf{T} \end{array} \right]$

Ahora sólo basta definir 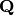$\mathbf{Q}$ como:

$\mathbf{Q}=\mathbf{U} \left[ \begin{array}{c|c} 1 & \mathbf{0} \\ \hline \mathbf{0} & \mathbf{V} \end{array} \right]$

Finalmente se tiene que:

$\mathbf{Q}^* \mathbf{A} \mathbf{Q} = \left[ \begin{array}{c|c} \lambda & \mathbf{BV} \\ \hline \mathbf{0} & \mathbf{T} \end{array} \right]$

que es de forma triangular superior.

De manera más general la descomposición de Schur se obtiene transformando 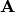$\mathbf{A}$ con una secuencia de transformaciones del tipo 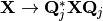$\mathbf{X} \to \mathbf{Q}_j^*\mathbf{X}\mathbf{Q}_j$ de manera que el producto

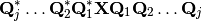
$\mathbf{Q}_j^* \dots \mathbf{Q}_2^*\mathbf{Q}_1^*\mathbf{X}\mathbf{Q}_1\mathbf{Q}_2 \dots \mathbf{Q}_j$

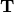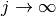converge a una matriz triangular superior $\mathbf{T}$ cuando $j \to \infty$ .

Dos fases para la factorización de Schur¶

El procedimiento anterior se realiza generalmente en dos fases:

1. Primero se produce una matriz de Hessenberg $\mathbf{H}$ que contiene ceros debajo de la primera subdiagonal.

2. Luego se realiza una iteración infinita de matrices de Hessenber para converger a una matriz triangular superior.

$\mathop{\left[ \begin{array}{ccccc} \times & \times & \times & \times & \times \\ \times & \times & \times & \times & \times \\ \times & \times & \times & \times & \times \\ \times & \times & \times & \times & \times \\ \times & \times & \times & \times & \times \\ \end{array} \right]}_{\mathbf{A}} \mathop{\xrightarrow{\hspace*{1cm}}}^{Fase 1} \mathop{\left[ \begin{array}{c c c c c} \times & \times & \times & \times & \times \\ \times & \times & \times & \times & \times \\ \, & \times & \times & \times & \times \\ \, & \, & \times & \times & \times \\ \, & \, & \, & \times & \times \\ \end{array} \right]}_{\mathbf{H}} \mathop{\xrightarrow{\hspace*{1cm}}}^{Fase 2} \mathop{\left[ \begin{array}{c c c c c} \times & \times & \times & \times & \times \\ \, & \times & \times & \times & \times \\ \, & \, & \times & \times & \times \\ \, & \, & \, & \times & \times \\ \, & \, & \, & \, & \times \\ \end{array} \right]}_{\mathbf{T}}$

Si a es hermitiana, la matriz de Hessenberg resulta tridiagonal y el resultado final es una matriz diagonal que contiene los valores propios:

$\mathop{\left[ \begin{array}{ccccc} \times & \times & \times & \times & \times \\ \times & \times & \times & \times & \times \\ \times & \times & \times & \times & \times \\ \times & \times & \times & \times & \times \\ \times & \times & \times & \times & \times \\ \end{array} \right]}_{\mathbf{A}=\mathbf{A}^*} \mathop{\xrightarrow{\hspace*{1cm}}}^{Fase 1} \mathop{\left[ \begin{array}{c c c c c} \times & \times & \, & \, & \, \\ \times & \times & \times & \, & \, \\ \, & \times & \times & \times & \, \\ \, & \, & \times & \times & \times \\ \, & \, & \, & \times & \times \\ \end{array} \right]}_{\mathbf{H}} \mathop{\xrightarrow{\hspace*{1cm}}}^{Fase 2} \mathop{\left[ \begin{array}{c c c c c} \times & \, & \, & \, & \, \\ \, & \times & \, & \, & \, \\ \, & \, & \times & \, & \, \\ \, & \, & \, & \times & \, \\ \, & \, & \, & \, & \times \\ \end{array} \right]}_{\mathbf{T}}$

Ejercicio propuesto¶

Encontrar la descomposición de Schur de la siguiente matriz:

$\begin{bmatrix} 7 & -2 \\ 12 & -3 \end{bmatrix}$

Clase 2: Algoritmos de Valores propios¶

Alternativa 1: Polinomio característico¶

Alternativa 2: Método de Iteración de Potencia¶

Otras Alternativas¶