Claudio Lobos
Home Meshing Publications Projects Tech. Rep.
[Español]
     
Introduction to meshing
Computer Assisted Simulation

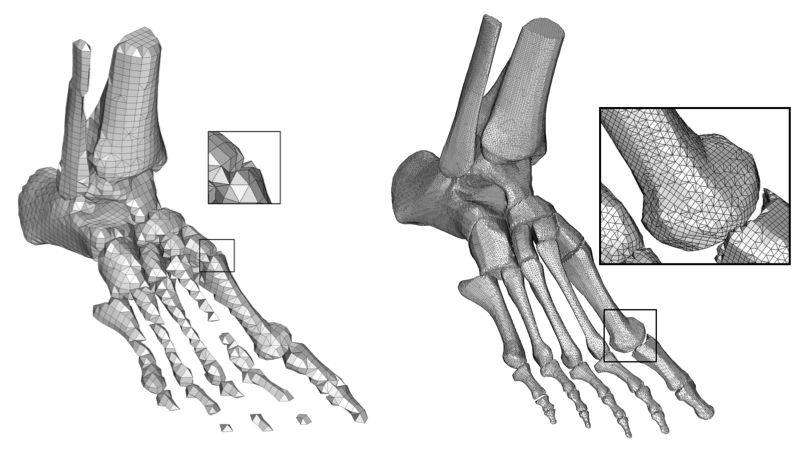
In order to computationally simulate an object, it is necessary to count with a function that describe it. When the geometry to simulate is complex, usually it is impossible to find such a mathematical function and therefore the overall geometry must be "approximated" by simpler geometries like hexahedra, prisms, pyramids, tetrahedra or a compound of these elements. The sum of all these elements describing a more complex geometry receives the name of a mesh.

The mesh can be used for visualization or simulation. In the first case, the inner nodes of the elements are not used and therefore it is possible to count with just a surface mesh, i.e., a mesh normally conformed by triangular and quadrilateral faces. Each face might present different visual properties like color, texture and transparency. The main application of surface meshes is in the entertainment industry like animated movies and computer games.

In the case of volumetric meshes (where inner non-visible elements of the mesh are used) the main application is the simulation of physical equations for structural analysis, deformations, fractures, the effect of heat, among others. Here the forces will be evaluated at the nodes of the elements and the final result of the simulation will be the sum of the local effects caused at each element. These type of simulations are described by a set of Partial Differential Equations (PDEs) and its solution is computed with numerical methods like Finite Elements, Finite Volumes or Finite Differences.

Two variables can be tuned to simulate the different types of materials: the stress and the stiffness. These properties can differ from one element to another causing different behaviors and therefore the simulation of the object.

Foot bones mesh

The above pictures show two a Volume Meshes of the foot bones. While the left model is less accurate, it allows to achieve fast simulation results. In the other hand, the right model should be employed when the accuracy of the simulation is the main focus.

Both are mixed-element meshes involving hexahedra, wedges (prisms), pyramids and tetrahedra.

This mesh can be used by the Finite Element Method to simulate foot pressure under particular circumstances.

Both meshes were extracted from the final engineering work of Pablo Riedemann where the focus was to produce meshes using the GPU as a powerful parallel processor. The left mesh was produced in 3 seconds while the right one took 1122 sec (18.7 minutes) with an "ordinary" computer (Intel Core i5 - 3.3 GHz and Nvidia GTX 570).