Clase 16: EDP Parabólicas¶
Bibliografía de la Clase:
- Introduction to Numerical Analysis - J.Stoer, R.Bulirsch. Chapter 7: Ordinary Differential Equations.
- Análisis Numérico - L. Burden, J Faires. Capítulo 12: Soluciones numéricas para las ecuaciones diferenciales parciales
- Guía profesor Luis Salinas 396
Ecuaciones diferenciales Parabólicas¶
Un ejemplo de EDP parabólica es la ecuación de calor o difusión:
Ecuación de calor o difusión
Usada para modelar el flujo de calor a lo largo de una varilla
de longitud  , en la cual la temperatura es uniforme en cada
sección transversal. Esta ecuación también es usada para
estudiar la difusión del gas.
, en la cual la temperatura es uniforme en cada
sección transversal. Esta ecuación también es usada para
estudiar la difusión del gas.
Ver la siguiente figura:

La EDP que modela este fenómeno es:
(1)
sujeta a las condiciones:
(2)
donde  es la conductividad del material,
es la conductividad del material,  es la
distribución de calor en el momento inicial y
es la
distribución de calor en el momento inicial y  y
y  son las
temperaturas constantes al inicio y el final de la varilla.
son las
temperaturas constantes al inicio y el final de la varilla.
Método Forward Difference¶
Al igual que en el caso anterior, se obtiene una expresión para las derivadas parciales usando las series de Taylor:

por lo tanto tenemos una expresión para:
(3)
Así también puede expresarse la segunda derivada parcial como:
(4)
Usando las ecuaciones (3) y (4) podemos expresar la ecuación (1) como:
(5)
Resolviendo la ecuación para  se obtiene un sistema de
ecuaciones:
se obtiene un sistema de
ecuaciones:
(6)
con  para
para  y
y  .
.
De las condiciones iniciales en (2) se tiene que:

La solución se va obteniendo para cada paso de tiempo  . Para
. Para
 la solución
la solución  se conoce y es:
se conoce y es:

La solución para el siguiente paso de tiempo está definida matricialmente por la ecuación (6):

donde

Ejercicio en clases¶
Aproxime la siguiente ecuación de calor usando  y
y  :
:

con las condiciones de borde:

El problema del método es que la estabilidad de su solución depende
de que el valor de 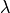 sea
sea  .
.
Método Backward Difference¶
Esta modificación surge para evitar que la efectividad del método
dependa de la condición  . La modificación consiste en
expresar la ecuación (6) ahora para resolver
. La modificación consiste en
expresar la ecuación (6) ahora para resolver  .
El cambio se realiza para la siguiente expresión:
.
El cambio se realiza para la siguiente expresión:
(7)
Usando esta expresión, ahora se tiene que:
(8)
El sistema de ecuaciones a resolver será entonces:

donde

En este caso también resolvemos  en función de
en función de
 . Sin embargo, en este caso la matriz
. Sin embargo, en este caso la matriz 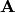 es positiva definida y estrictamente diagonal lo que asegura
estabilidad en la solución.
es positiva definida y estrictamente diagonal lo que asegura
estabilidad en la solución.
Ejercicio propuesto¶
Programe el ejercicio en clases usando el método Forward and Backward
Difference  y para dos valores de
y para dos valores de 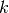 :
:  y
y  hasta
hasta  . Compare el error de ambos métodos considerando que la
solución analítica es:
. Compare el error de ambos métodos considerando que la
solución analítica es:

Concluya en términos de 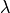 .
.
