Clase 15: Ecuaciones diferenciales parciales¶
Bibliografía de la Clase:
- Introduction to Numerical Analysis - J.Stoer, R.Bulirsch. Chapter 7: Ordinary Differential Equations.
- Análisis Numérico - L. Burden, J Faires. Capítulo 12: Soluciones numéricas para las ecuaciones diferenciales parciales
- Guía profesor Luis Salinas 396
Introducción a EDP¶
Una ecuación diferencial parcial (EDP) es una ecuación que contiene
una función multivariable desconocida (ej.  ) y sus derivadas
parciales. Este tipo de ecuaciones describen varios fenómenos físicos
como el calor, el sonido, dinámica de fluidos, etc.
) y sus derivadas
parciales. Este tipo de ecuaciones describen varios fenómenos físicos
como el calor, el sonido, dinámica de fluidos, etc.
El orden de la EDP está determinado por el grado de la derivada parcial más alto.
Una EDP de segundo orden genérica tiene la forma:

en una cierta región  . Se dice que la EDP
es de tipo:
. Se dice que la EDP
es de tipo:
- Hiperbólica: si
en
.
- Parabólica: si
en
.
- Elíptica: si
en
.
Ecuaciones diferenciales Elípticas¶
Ejemplos de EDP elípticas son la ecuación de Poisson y Laplace:
Ecuación de Poisson
Usada en el estudio de problemas físicos como distribución de calor, energía potencial sobre un punto y dinámica de fluidos.
(1)
donde f(x,y) es una función definida sobre una región  con borde
con borde 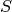 .
.
La ecuación de Poison es del tipo elíptica ya que  y
y  ,
por lo tanto
,
por lo tanto  .
.
Esta ecuación es equivalente a:

donde  es el operador de Laplace o Laplaciano:
es el operador de Laplace o Laplaciano:

Ecuación de Laplace
es un caso particular de la ecuación de
Poisson donde  que significa que la región
que significa que la región  es plana.
es plana.

Si el valor de  en la región
en la región  es determinada por el valor
de la función en el borde
es determinada por el valor
de la función en el borde 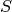 se les denomina condiciones de borde
de Dirichlet que viene dado por:
se les denomina condiciones de borde
de Dirichlet que viene dado por:


En la figura, la región  está definida como:
está definida como:

Métodos numéricos para EDP¶
Para resolver numéricamente este tipo de ecuaciones se utiliza una
adaptación del método de diferencias finitas. El método consiste en
generar una grilla equiespaciada en la región  para obtener
aproximaciones de la función en los puntos de la grilla
para obtener
aproximaciones de la función en los puntos de la grilla  iterativamente.
iterativamente.
El número de puntos de la grilla para 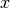 e
e  son
son 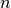 y
y 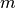 respectivamente, por lo tanto el espaciado entre los puntos es:
respectivamente, por lo tanto el espaciado entre los puntos es:


Para expresar numéricamente  e
e  se utiliza la serie
de Taylor alrededor de
se utiliza la serie
de Taylor alrededor de  . De manera aproximada se tiene:
. De manera aproximada se tiene:

y luego se suman para obtener una expresión para  :
:

Aproximaciones usando series de Taylor¶
Podemos usar las expansiones de Taylor mostradas anteriormente para resolver la ecuación de Poisson expresando:

ahora podemos expresar la ecuación (1) en el punto (x_i,y_j) aproximadamente como:

Agrupando términos, y expresando  se tiene:
se tiene:
(2)![\boxed{
2\Big[ \Big( \frac{h}{k}\Big)^2+1\Big] u_{i,j} -
u_{i+1,j}-u_{i-1,j} -
\Big( \frac{h}{k}\Big)^2 \big( u_{i,j+1} + u_{i,j-1} \big)
= -h^2 f(x_i,y_j)}](_images/math/375a19d36749f00115fae8a8dcce54ef421bb248.png)
Para definir las condiciones de borde, se debe especificar que el
valor de  en la frontera está definido por la función
en la frontera está definido por la función
 .
.
(3)
Las ecuaciones (2) y (3) definen un sistema de ecuaciones que puede ser representado matricialmente.
Ejercicio en clases¶
Determine la distribución del calor en estado estable en una
superficie metálica de dimensiones  utilizando una
grilla de tamaño
utilizando una
grilla de tamaño  . Las condiciones de borde en los ejes
. Las condiciones de borde en los ejes 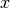 e
e
 son 0 y el calor en los otros dos bordes crece linealmente desde
0 a 100 grados.
son 0 y el calor en los otros dos bordes crece linealmente desde
0 a 100 grados.
Ejercicio propuesto 1¶
Estudie cómo se utiliza el método de Gauss Seidel para encontrar los
 y encuentre la solución de la ecuación (5).
Encuentre el error asociado al método numérico considerando que la
solucíón analítica es
y encuentre la solución de la ecuación (5).
Encuentre el error asociado al método numérico considerando que la
solucíón analítica es  .
.
Ejercicio propuesto 2¶
En un recinto cuadrado de lado 1 considere la ecuación de Poisson:

con condición de borde igual a cero en los cuatro costados. Encuentre
la solución de este problema usando el método de diferencias finitas,
considerando  .
.






 :
:
 :
:













