Clase 3: Reducción de Hessenberg¶
Bibliografía de la Clase:
- Numerical Linear Algebra.L.N. Trefethen. Chapter 5: Lecture 26 Reduction of Hessenberg or Tridiagonal Form
- Guía profesor Luis Salinas
Matriz de Hessenberg¶
La matriz de Hessenberg de una matriz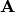 
tiene la siguiente forma:
![\mathop{\left[ \begin{array}{c c c c c} \times & \times &
\times & \times & \times \\ \times & \times & \times & \times
& \times \\ \, & \times & \times & \times & \times \\ \, & \,
& \times & \times & \times \\ \, & \, & \, & \times & \times
\\ \end{array} \right]}_{\mathbf{H}}](_images/math/86bc36a4303be12e00ca6264f5bbc260d8fc98ae.png)
Esta matriz se define como:
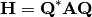
donde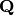 
es una matriz unitaria y 
es la matriz
de Hessenberg.
Nota
Recordar que la matriz de Hessenberg se obtiene como un paso
intermedio para obtener la factorización de Schur que revela
los valores propios de .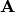
La estrategia para construir la matriz de Hessenberg
es introducir ceros bajo la subdiagonal:
![\mathop{\left[ \begin{array}{ccccc}
\times & \times & \times & \times & \times \\
\times & \times & \times & \times & \times \\
\times & \times & \times & \times & \times \\
\times & \times & \times & \times & \times \\
\times & \times & \times & \times & \times \\
\end{array} \right]}_{\mathbf{A}}
\mathop{\xrightarrow{\hspace*{1cm}}}^{\mathbf{Q}_1^* \cdot}
\mathop{\left[ \begin{array}{c c c c c}
\times & \times & \times & \times & \times \\
\ast & \ast & \ast & \ast & \ast \\
0 & \ast & \ast & \ast & \ast \\
0 & \ast & \ast & \ast & \ast \\
0 & \ast & \ast & \ast & \ast \\
\end{array} \right]}_{\mathbf{Q_1^* A}}
\mathop{\xrightarrow{\hspace*{1cm}}}^{\cdot \mathbf{Q}_1}
\mathop{\left[ \begin{array}{c c c c c}
\times & \diamond & \diamond & \diamond & \diamond \\
\ast & \diamond & \diamond & \diamond & \diamond \\
0 & \diamond & \diamond & \diamond & \diamond \\
0 & \diamond & \diamond & \diamond & \diamond \\
0 & \diamond & \diamond & \diamond & \diamond \\
\end{array} \right]}_{\mathbf{Q_1^* A Q_1}}](_images/math/74bab59a69cc9e2e79836e54d93523794e6dc122.png)
Se debe encontrar una matr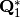iz 
que cuyo efecto al
multiplicar a la matriz 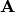sea crear ceros bajo la
subdiagonal y que este resultado al premultiplicarse por
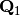mantenga los ceros creados. Este proceso debe repitirse
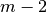veces. Finalmente se obtendrá la matriz de Hessenberg como:
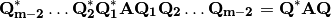
Reducción de Householder¶
La construcción de las matrices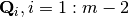 
está basada en
la idea de los reflectores de Householder (Ver Clase Householder):
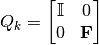
donde,
es la matriz identidad de dimensión
.
es el Reflector de Householder de dimensión
, y es una matriz unitaria.
tiene dimensión
Nota
Recuerde que el reflector de Householder 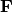se obtiene como
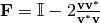y su
efecto sobre un vector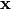 
es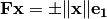 
.
El algoritmo que resume el procedimiento es el siguiente:
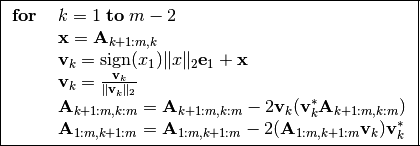
En el algoritmo puede apreciarse que nunca se calculan explícitamente
las matrices 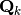pero éstas pueden ser obtenidas a partir
de los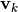 
.
Ejercicio en clases¶
Demostrar gráficamente que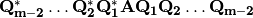 
tiene forma tridiagonal.
Ejercicio propuesto¶
Explique cuál es la relación de las matrices 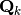usadas
para encontrar la matriz de Hessenberg con respecto a las usadas en la
triangularización de Householder. Hint: Leer introducción Lecture 26 y
Lecture 10 del texto guía Numerical Linear Algebra, Trefethen.
