Clase 5: Método de Iteración Inversa¶
Bibliografía de la Clase:
- Numerical Linear Algebra. L.N. Trefethen. Chapter 5, Lecture 27: Rayleigh Quotient, Inverse Iteration
- Guía Profesor Luis Salinas
Introducción¶
Sea  tal que
tal que  , i.e.,
, i.e., 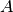 es real y simétrica, de modo que sus
es real y simétrica, de modo que sus 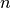 valores propios
valores propios  son reales y distintos, y el sistema de sus
son reales y distintos, y el sistema de sus 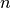 vectores propios
vectores propios  constituye una base ortogonal de
constituye una base ortogonal de  .
.
Entonces, para todo  que no es un valor propio de
que no es un valor propio de 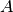 se tiene:
se tiene:
Los vectores propios dey
coinciden con los vectores propios de
, y tienen valores propios
y
, respectivamente.
Detalle¶
- Si
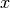 en un vector propio de la matriz
en un vector propio de la matriz 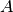 , y
, y 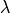 es su vector propio asociado. Para la matriz
es su vector propio asociado. Para la matriz  se tiene:
se tiene:

- Por lo tanto
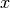 es un vector propio de
es un vector propio de  , y
, y  es su valor propio.
es su valor propio.
Ejemplo¶

Desarrollo¶
¿Cuáles son los valores propios y vectores propios de
 ,
,  ?
?- Utilizando alguno de los métodos conocidos para el cálculo de valores propios, se obtiene
 y
y  para la matriz
para la matriz 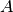 .
. - Por lo tanto,
 y
y  son los valores propios de
son los valores propios de  ,
,  y
y  son los valores propios de
son los valores propios de  .
. - Los vectores propios son iguales para las tres matrices.
- Utilizando alguno de los métodos conocidos para el cálculo de valores propios, se obtiene
Iteración Inversa¶
Nota
El algoritmo de Iteración inversa hace lo mismo que el Método de Potencias, pero usa la matriz 

Idea¶
- Suponer que
 es muy próximo a un valor propio
es muy próximo a un valor propio  de
de 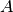
 es el spectrum o conjunto de los valores propios de
es el spectrum o conjunto de los valores propios de 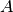 .
.- Un vector arbitrario
 se puede expresar en términos de la base
se puede expresar en términos de la base  :
:


Además (por el algoritmo,  )
)
![v^{(k)}= \text{const.} (A-\mu I)^{-p} v^{(0)}
v^{(k)}= \text{const.}[ c_1 (\lambda_1 - \mu)^{-p} V_1 + c_2 (\lambda_2 - \mu)^{-p} V_2 + \dots + c_n (\lambda_n - \mu)^{-p} V_n]](_images/math/27f3a70a80735dce2e9cfff2b9376b4007fc7b08.png)
Si  es dominante en la suma
es dominante en la suma

- Si
 es cercano a
es cercano a  es dominante en la suma
es dominante en la suma - El algoritmo tiende al valor propio de
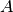 , porque todas las matrices
, porque todas las matrices  tienen los mismos vectores propios.
tienen los mismos vectores propios.

Ejemplo¶
Se tiene la matriz 
Utilizando el siguiente código (simplificado) analice la salida del algoritmo utilizando como entrada:
 y
y 
 y
y 
1 2 3 4 5 6 7 8 9 10 11 12 | function [lambda,v]= simpleInverseIteration(A,v,mu,steps)
v=v/norm(v);
n=size(A,1);
for i=1:steps
A_new= A-mu*eye(n);
w=A_new\v;
v=w/norm(w);
lambda=v'*A*v;
end
|
Teorema:
Suponer que  es el valor propio más cercano a
es el valor propio más cercano a  y
y  es el segundo más cercano, es decir,
es el segundo más cercano, es decir,  . Además, suponer que
. Además, suponer que  . Entonces las iteraciones del algoritmo Iteración Inversa, satisface:
. Entonces las iteraciones del algoritmo Iteración Inversa, satisface:

cuando  .
.
Iteración del Cuociente de Rayleigh¶
- Utilizando el cuociente de Rayleigh se obtiene la aproximación de un valor propio, a partir de un vector propio estimado
- De la iteración inversa se obtiene un vector propio a partir de un valor propio estimado.
- La combinación de ambas ideas da origen al algoritmo de Iteración del Cuociente de Rayleigh:

La convergencia de este algoritmo es mucho mejor: cada iteración triplica el número de digitos de la precisión.
Ejemplo
- Se tiene la matriz
 y
y 
- Encontrar el valor propio correspondiente al vector propio más cercano a
 .
.
1 2 3 4 5 6 7 8 9 10 11 12 | function [lambda,v]= simpleRayleighIteration(A,v,steps)
v=v/norm(v);
lambda=v'*A*v;
n=size(A,1);
for i=1:steps
A_new= A-lambda*eye(n);
w=A_new\v;
v=w/norm(w);
lambda=v'*A*v;
end
|
Ejercicio Propuesto¶
- Dada la matriz
 y
y  explique y desarrolle el algorimto de iteración inversa para encontrar un vector propio.
explique y desarrolle el algorimto de iteración inversa para encontrar un vector propio.
