Clase 6: Iteración simultánea y algoritmo de QR¶
Bibliografía de la Clase:
- Numerical Linear Algebra.L.N. Trefethen. Chapter 5: Lecture 28 QR Algorithm without Shifts
- Guía profesor Luis Salinas
Iteración Simultánea¶
El método de iteración de potencia (visto en la clase
Clase 2)
sólo permite encontrar un valor propio de la matriz 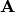 .
.
El método de iteración simultánea (o método de iteración
de potencia por bloques) extiende el método de iteración de potencia
para poder encontrar los 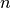 vectores propios
(
vectores propios
( ) asociados a los
) asociados a los 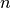 valores propios de
mayor valor absoluto (
valores propios de
mayor valor absoluto ( ).
La idea consiste en aplicar el método de iteración de potencia a
varios vectores a la vez.
).
La idea consiste en aplicar el método de iteración de potencia a
varios vectores a la vez.
Inicialmente ahora se cuenta con un set de 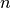 vectores linealmente
independientes
vectores linealmente
independientes  .
.
Si los agrupamos matricialmente se tiene:
![\mathbf{V^{(0)}} =
\left[ \begin{array}{c|c|c}
\, & \, & \, \\
\mathbf{v}_1^{(0)} & \cdots & \mathbf{v}_n^{(0)} \\
\, & \, & \,
\end{array}
\right]](_images/math/f11eb5f88b50861acfbe36554565dca7cebcfd45.png)
Al ir multiplicando sucesivamente por 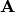 se tiene que en la
iteración
se tiene que en la
iteración 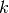 usando el método de iteración de potencia se tendrá:
usando el método de iteración de potencia se tendrá:
![\mathbf{V}^{(k)} = \mathbf{A^k V^{(0)}} =
\left[ \begin{array}{c|c|c}
\, & \, & \, \\
\mathbf{v}_1^{(k)} & \cdots & \mathbf{v}_n^{(k)} \\
\, & \, & \, \end{array}
\right]](_images/math/0a05edd611aabb66247c207788336115b7a6700d.png)
Si expandimos los vectores  y
y  en los valores propios de
en los valores propios de 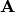 se tiene:
se tiene:

Lo que se espera de este procedimiento es que todas las columnas de
 tiendan a
tiendan a  (vector propio asociado al
valor propio de mayor valor). Para evitar esto, se fuerza a que los
vectores
(vector propio asociado al
valor propio de mayor valor). Para evitar esto, se fuerza a que los
vectores  sean
ortonormales en cada iteración (originalmente en el algoritmo de
iteración de potencia se normalizaban los vectores encontrados).
La ortonormalización se realiza usando la descomposición QR de las
matrices
sean
ortonormales en cada iteración (originalmente en el algoritmo de
iteración de potencia se normalizaban los vectores encontrados).
La ortonormalización se realiza usando la descomposición QR de las
matrices  .
.
Nota
La matriz 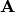 debe ser real y simétrica.
debe ser real y simétrica.
El algoritmo de la iteración simultánea es el siguiente:

Una pequeña modificación del algoritmo corresponde a:

Los cambios realizados son:
- Se reemplazó
por
para poder diferenciar las matrices
generadas por el algoritmo de iteración simultánea.
- Se definieron las matrices
y
(líneas 3 y 4) para poder compararlo posteriormente con el algoritmo de QR.
Condiciones¶
La convergencia del algoritmo depende de dos condiciones:
- La matriz
tiene
vectores propios ortogonales
con los correspondientes valores propios
- Todos los menores principales de
son no singulares. Los menores principales corresponden a las submatrices cuadradas izquierdas superiores de dimensiones
,
, etc.
Nota
Notar que la matriz  corresponde
a los coeficientes
corresponde
a los coeficientes  .
.
Ejercicio propuesto
- Probar que la matriz
corresponde a la matriz de los coeficientes
.
Este método, aunque funciona, no es usado generalmente en la práctica ya que existe un algoritmo que realiza las mismas operaciones de una forma más elegante que el método de iteración simultánea, el algoritmo QR.
Primera versión: Algoritmo QR¶
El algoritmo QR es usado para poder construir una matriz triangular
superior a partir de una matriz 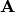 (Fase 2 vista en la
Clase 3). El algoritmo mejora su tasa de
convergencia si recibe como entrada una matriz de Hessenberg
(Fase 2 vista en la
Clase 3). El algoritmo mejora su tasa de
convergencia si recibe como entrada una matriz de Hessenberg
 .
.
El algoritmo QR puede ser utilizado para encontrar la matriz diagonal superior de la descomposición de Schur. De la Clase 3 vimos que si queremos obtener ceros bajo la diagonal usando el siguiente procedimiento:

resultaba que al postmultiplicar por la matriz 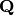 se destruían los
ceros formados.
se destruían los
ceros formados.
Sin embargo, el procedimiento anterior resulta ser efectivo cuando se realiza iterativamente:

La idea del algoritmo es ir obteniendo una matriz diagonal superior en dos pasos:
- Primero se calcula
(línea 1),
- Y luego se obtiene
(línea 2) que equivale a
, es decir se está pre y post multiplicando sucesivamente por matrices ortonormales.
Nota
De lo anterior resulta que  es similar a
es similar a
 y por lo tanto a
y por lo tanto a 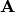 , es decir,
todas ellas tienen los mismos valores propios.
, es decir,
todas ellas tienen los mismos valores propios.
Para poder comparar el algoritmo QR con el método de iteración simultánea se han
definido dos matrices adicionales que no afectan el algoritmo:
 y
y  (líneas 3 y 4).
(líneas 3 y 4).

