Contenidos
Tema anterior
Clase 16: Más de Mínimos Cuadrados
Próximo tema
Clase 18: Representación de Punto Flotante
Esta página
Búsqueda rápida
Enter search terms or a module, class or function name.
Bibliografía de la Clase:
- Numerical Linear Algebra.L.N. Trefethen. Part III: Lecture 12 Conditioning and Condition Numbers
Condicionamiento
Es la sensibilidad o perturbación de un problema matemático que
puede verse como una función 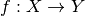 , donde
, donde 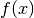 es
una instancia del problema.
es
una instancia del problema.
Estabilidad
Se refiere a la sensibilidad o perturbación de un algoritmo para resolver un problema.
Un problema se dice bien condicionado si pequeñas perturbaciones de  conllevan a pequeños cambios en
conllevan a pequeños cambios en 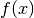 , de lo contrario se dice mal condicionado.
, de lo contrario se dice mal condicionado.
Para cuantificar el tamaño de una perturbación pequeña en  denominada
denominada 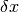 de un problema se utilizan los números
de condición. Se define
de un problema se utilizan los números
de condición. Se define 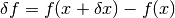 como el efecto de
como el efecto de 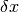 en la función
en la función 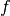 .
.
Existen dos números de condición:
- Número de condición absoluto teniendo en cuenta que
y
son infinitesimales:
Si la función
es diferenciable, podemos evaluar
obteniendo las derivadas parciales de
, en este caso puede definirse
y
donde la norma es inducida sobre
y
.
- Número de condición relativo se usa cuando interesan los cambios relativos.
Debido a que los computadores introducen errores relativos,
es más usado en la práctica que
.
Nota
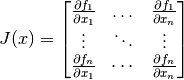
El Jacobiano es una matriz que contiene todas las
derivadas parciales de primer orden de una función 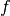 .
.
Ejemplos
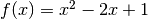
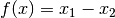 donde
donde ![x=[x_1,x_2]^T](_images/math/ed514a86f399c0e70649bc8cafb4d873fbdc939e.png) .
.Se le denomina 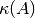 al número de condición de la matriz A, donde:
al número de condición de la matriz A, donde:
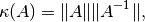
donde  es una norma matricial.
es una norma matricial.
Si 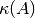 es grande (ej:
es grande (ej: 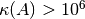 ) se dice que
) se dice que  es una
matriz mal condicionada. Se dirá que
es una
matriz mal condicionada. Se dirá que  está bien condicionada
en el caso contrario.
está bien condicionada
en el caso contrario.
El problema es entonces 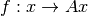 y la perturbacion
y la perturbacion 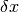 .
La perturbación de
.
La perturbación de 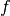 sería entonces
sería entonces
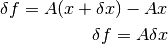
Con esta información, podemos encontrar el número de condición relativo del problema 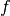 :
:
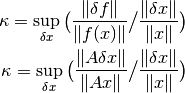
pero sabemos que 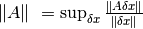 que es la definición de la norma inducida de una matriz. Entonces se tiene que:
que es la definición de la norma inducida de una matriz. Entonces se tiene que:
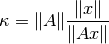
El número de condición relativo  se simplifica cuando
se simplifica cuando  es invertible
ya que se cumple que:
es invertible
ya que se cumple que:
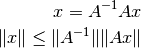
de esta manera podemos reescribir  como:
como:
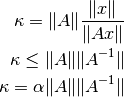
donde  puede elegirse convenientemente de manera que
puede elegirse convenientemente de manera que 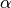 sea igual a
sea igual a 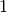 .
.
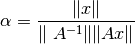
finalmente decirmos que 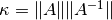 .
.
Nota
El caso de matrices cuadradas de 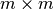 ,
,
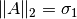 y
y 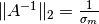 .
Por lo tanto
.
Por lo tanto 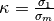 .
.
Si  no es invertible el procedimiento es análogo, pero ahora usando la pseudoinversa:
no es invertible el procedimiento es análogo, pero ahora usando la pseudoinversa:
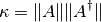
Perturbación en 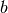
Ahora el problema es el cálculo de  dado
dado 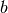 , es decir:
, es decir: 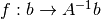 donde su número de condición cuando perturbamos
donde su número de condición cuando perturbamos 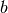 (no
(no  como en el caso anterior) se obtiene de manera análoga y es también
como en el caso anterior) se obtiene de manera análoga y es también 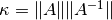 .
.
En el caso anterior analizamos el efecto de perturbar  o
o 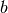 separadamente.
Ahora se analizará el efecto de perturbar
separadamente.
Ahora se analizará el efecto de perturbar  en
en  manteniendo
manteniendo 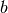 fijo:
fijo:
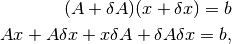
considerando que 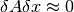 se tiene:
se tiene:
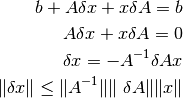
Entonces el cálculo del número de condición relativo es:
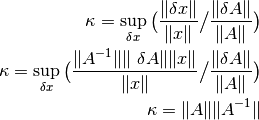
Ejercicio propuesto
- Sea
con
y
. Determine una cota mínima para el número de condición
definido en
.
- Dada la matriz
determine los números de condición relativos
y
para el cálculo de los valores propios de
..