Contenidos
Tema anterior
Próximo tema
Esta página
Búsqueda rápida
Enter search terms or a module, class or function name.
Bibliografía de la Clase
- Numerical Linear Algebra. L.N. Trefethen. Chapter 2, Lecture 11: Least Squares Problems
- Guía profesor Luis Salinas
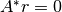 y
y 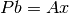
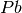 es la proyección ortogonal de
es la proyección ortogonal de 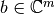 sobre
sobre 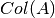 , i.e.,
, i.e., 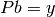 , donde
, donde 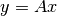 para algún
para algún 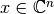 , por lo tanto
, por lo tanto 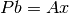 .
.
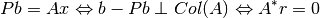
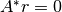 y
y 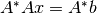 :
: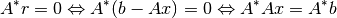
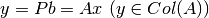
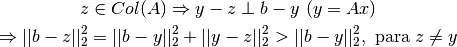

Además,
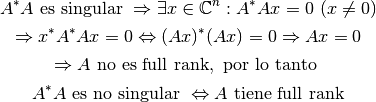
Por otro lado,
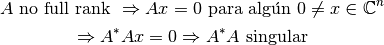
Por lo tanto,
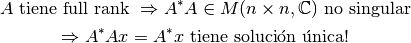
Si  es full rank, la solución de
es full rank, la solución de  está dada por:
está dada por:
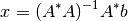
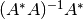 se denomina la pseudoinversa de
se denomina la pseudoinversa de  , y se denota
, y se denota 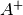 .
.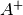 transforma el vector
transforma el vector 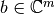 al vector
al vector 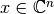 , lo que explica que
, lo que explica que 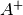 tiene dimensión
tiene dimensión 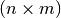 (más columnas que filas).
(más columnas que filas).Resumiendo:
El problema de mínimos cuadrados consiste en calcular alguno de los sgtes. vectores:
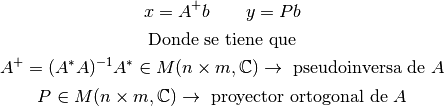
¿Cómo calcular los vectores  e
e 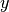 ?
?
Utilizando las ecuaciones normales: 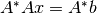
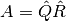
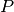 puede ser de la forma:
puede ser de la forma: 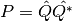 , que permite obtener la proyección de
, que permite obtener la proyección de 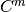 sobre
sobre 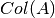 .
.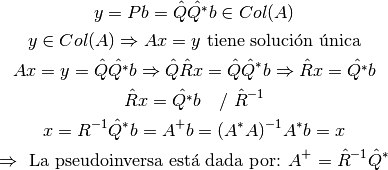
Ventajas