Bibliografía de la Clase:
- Numerical Linear Algebra.L.N. Trefethen. Part III: Lecture 14 Stability
Los algoritmos numéricos no proveen soluciones exactas a todos los problemas numéricos debido a que la mayoría de los problemas son continuos y los computadores trabajan de manera discreta. El estudio de la estabilidad de un algoritmo nos permite medir su capacidad de obtener una respuesta correcta (accuraccy) aunque ésta no sea exacta (precision).
Precisión
Corresponde a la finura de detalle con que se representa un número o medida, es decir a las cifras significativas. Este concepto se relaciona con el tamaño de las unidades usadas para hacer una medición, mientras más pequeña sea la unidad, mayor precisión.
Exactitud (Accuracy)
Corresponde a la diferencia entre una medición y el valor real aceptado como correcto. Mientas menor sea dicha diferencia, mayor será su exactitud o accuracy.
Anteriormente definimos un problema matemático como una función:
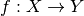
y un algoritmo como:
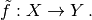
Para determinar la aproximación del algoritmo al problema asociado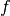 
se
definen dos tipos de error:
Error absoluto
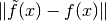
Error relativo
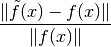
Si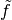 
es un buen algoritmo se espera que el error relativo sea
pequeño, del orden de 
machine. Es decir:
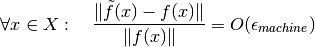
Si 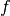es un problema mal condicionado la medición de la exactitud o accuracy
es muy ambiciosa. Una medida menos estricta es la estabilidad que se cumple
cuando:
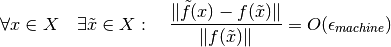
donde:
