Clase 1: Valores Propios y Vectores Propios¶
Bibliografía de la Clase:
- Numerical Linear Algebra. L.N. Trefethen. Chapter 5, Lecture 24: Eigenvalue Problems
- Introduction to Linear Algebra. Gilbert Strang. Chapter 6 Eigenvalues and Eigenvectors
- Guía Profesor Luis Salinas
Introducción¶
Un breve recordatorio de valores y vectores propios:
Sea 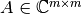 una matriz cuadrada. Un vector
una matriz cuadrada. Un vector 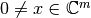 es un vector propio (eigenvector) de
es un vector propio (eigenvector) de 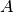 , y
, y 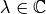 es su valor propio (eigenvalue) correspondiente, si:
es su valor propio (eigenvalue) correspondiente, si:
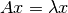
La idea principal es que la transformación que aplica la matriz
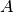 en el subespacio
en el subespacio 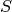 de
de 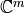 puede algunas veces imitar una multiplicación por un escalar.
puede algunas veces imitar una multiplicación por un escalar.Cuando lo anterior sucede, el subespacio
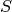 es llamado espacio propio (eigenspace), y cualquier vector
es llamado espacio propio (eigenspace), y cualquier vector 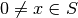 es un vector propio.
es un vector propio.El conjunto de valores propios de la matriz
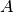 se denomina spectrum de
se denomina spectrum de 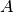 , y es un subconjunto de
, y es un subconjunto de 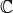 y se denota
y se denota 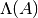 .
.- Los valores y vectores propios son útiles por dos razones: algorítmica y física.
- Algorítmicamente, el análisis de valores propios puede simplificar soluciones de ciertos problemas reduciendo un sistema acoplado a una colección de problemas escalares (por ej., encontrar la potencia
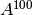 ).
). - Físicamente, en análisis de valores propios puede ayudar a la resolución de sistemas que evolucionan que se rigen por ecuaciones lineales (por ej., estudio de la resonancia).
- Algorítmicamente, el análisis de valores propios puede simplificar soluciones de ciertos problemas reduciendo un sistema acoplado a una colección de problemas escalares (por ej., encontrar la potencia
Mayor detalle en Valores y Vectores Propios
Ejercicio en clases 1.1¶
Sea 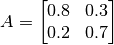 . Obtener
. Obtener 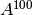 .
.
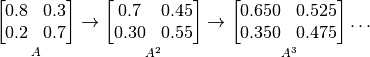
- El valor de
 se puede encontrar usando los valores propios y no haciendo 100 multiplicaciones.
se puede encontrar usando los valores propios y no haciendo 100 multiplicaciones. - Primeramente, se deben encontrar los valores y vectores propios de
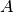 :
: 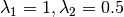 y
y ![v_1=[0.6 \quad 0.4]^T, v_2=[1 \quad -1]^T](_images/math/787ebfcf63cac9c72b5559762d64162f2458c1c6.png) , son respectivamente sus valores y vectores propios.
, son respectivamente sus valores y vectores propios. - Si se multiplica
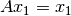 , y con cada potencia de
, y con cada potencia de 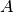 se obtendrá
se obtendrá 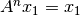 . Al multiplicar
. Al multiplicar 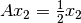 y si se sigue multiplicando se obtiene
y si se sigue multiplicando se obtiene 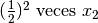 .
. - Debido a que
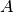 tiene
tiene 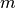 valores propios distintos, por lo tanto,
valores propios distintos, por lo tanto, 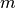 vectores propios lindealmente independientes, se puede encontrar la primera columna de
vectores propios lindealmente independientes, se puede encontrar la primera columna de 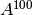 mediante una combinación lineal de los vectores propios:
mediante una combinación lineal de los vectores propios:
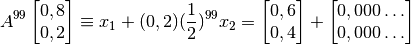
Lo mismo para la segunda columna de 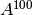 , por lo tanto:
, por lo tanto:
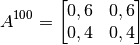
Nota
La matriz 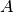 anterior es una Matriz de Markov. Todas sus entradas son positivas y los elementos de cada columna suman 1. Esto garantiza que el mayor valor propio es 1 lo que indica que el el vector propio no cambia su estado (porque
anterior es una Matriz de Markov. Todas sus entradas son positivas y los elementos de cada columna suman 1. Esto garantiza que el mayor valor propio es 1 lo que indica que el el vector propio no cambia su estado (porque 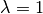 ) y por lo tanto el otro vector propio decae, hasta desaparecer, mientras mayor sea la potencia de
) y por lo tanto el otro vector propio decae, hasta desaparecer, mientras mayor sea la potencia de 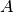 .
.
Revisar Ejercicio Propuesto
Descomposición de Valores Propios¶
La descomposición de valores propios de una matriz cuadrada 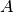 , es la factorización:
, es la factorización:
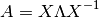
Esta factorización, no siempre existe. 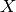 es no singular y
es no singular y 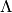 es diagonal.
es diagonal.
Esta factorización puede también ser escrita como:
![\begin{bmatrix}
\quad & \quad & \quad\\
\quad & A & \quad\\
\quad & \quad & \quad
\end{bmatrix}
\left[ \begin{array}{c|c|c|c}
\, & \, & \, & \, \\
x_1 & x_2 & \cdots & x_m \\
\, & \, & \, & \,
\end{array} \right]=
\left[ \begin{array}{c|c|c|c}
\, & \, & \, & \, \\
x_1 & x_2 & \cdots & x_m \\
\, & \, & \, & \,
\end{array} \right]
\begin{bmatrix}
\lambda_1 & \, & \, & \, \\
\, & \lambda_2 & \, & \, \\
\, & \, & \ddots & \, \\
\, & \, & \, & \lambda_m
\end{bmatrix}](_images/math/a6f898b5d53e8507eb4e7cdc5339e855d2581a19.png)
En una notación más resumida:
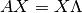
Transformación de Similitud¶
Si 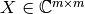 es no singular, entonces la transformación
es no singular, entonces la transformación 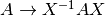 se denomina transformación de similitud de
se denomina transformación de similitud de 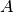 . Se dice que dos matrices
. Se dice que dos matrices 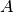 y
y 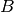 son similares si hay una transformación de similitud que las relacione, es decir, si existe una matriz
son similares si hay una transformación de similitud que las relacione, es decir, si existe una matriz 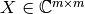 no singular tal que:
no singular tal que:
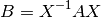
Matrices Deficientes y Diagonalización¶
En general, una matriz tiene multiplicidades geométrica y algebraica iguales, pero no ocurre para todas las matrices.
Si se consideran las siguientes matrices:
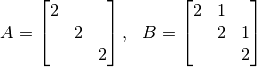
Ambas matrices tienen polinomios característicos 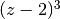 , por lo tanto, hay
un solo valor propio
, por lo tanto, hay
un solo valor propio 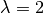 que tiene multiplicidad algebraica 3.
Para la matriz
que tiene multiplicidad algebraica 3.
Para la matriz 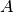 se pueden escoger tres vectores propios independientes, por
ejemplo,
se pueden escoger tres vectores propios independientes, por
ejemplo, 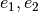 y
y 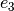 , por lo tanto la multiplicidad geométrica también
es 3.
, por lo tanto la multiplicidad geométrica también
es 3.
Para la matriz 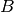 , se puede encontrar solo un vector propio independiente
(
, se puede encontrar solo un vector propio independiente
(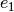 ), por lo tanto la multiplicidad geométrica del valor propio es 1.
), por lo tanto la multiplicidad geométrica del valor propio es 1.
Un valor propio cuya multiplicidad algebraica excede su multiplicidad geométrica se dice que es un valor propio deficiente. Una matriz que tiene uno o más valores propios deficientes se denomina matriz deficiente.
Toda matriz diagonal es no deficiente. En estas matrices, la multiplicidad
algebraica y geométrica de un valor propio 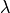 son iguales al número de ocurrencias en la diagonal.
son iguales al número de ocurrencias en la diagonal.
La clase de matrices no deficientes son precisamente la clase de matrices que tienen una descomposición de valores propios. En otras palabras las matrices no deficientes son diagonalizables.
La diagonalización de matrices corresponde a una transformación de similitud.
Nota
De CC1: La multiplicidad geométrica corresponde a la dimensión del subespacio propio generado por el valor propio 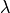 (o al número de vectores propios l.i. asociado a
(o al número de vectores propios l.i. asociado a 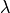 ). La multiplicidad algebraica corresponde al número de veces que aparece el valor propio
). La multiplicidad algebraica corresponde al número de veces que aparece el valor propio 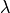 como raíz de la ecuación característica de A.
como raíz de la ecuación característica de A.
¿Para que es útil la diagonalización? Nuevamente consideremos 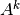 :
:
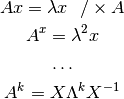
Ejercicio 1.2. Números de Fibonacci¶
- Hallar el número de Fibonacci
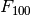 .
.
Los números de Fibonacci está formada por los números: 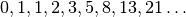 . Se definen recursivamente como:
. Se definen recursivamente como:
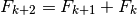
Pero se quisiera lograr una ecuación de la forma:
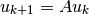
para usar las ventajas de los valores y vectores propios. Como 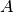 tiene
tiene  valores propios distintos (por lo tanto
valores propios distintos (por lo tanto 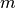 vectores propios,
vectores propios, 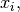 l.i.) y
l.i.) y 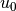 es conocido (condición inicial):
es conocido (condición inicial):
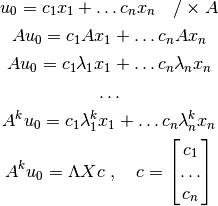
Tomando en cuenta lo anterior, se puede usar el truco: 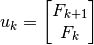 . Con esta definición se puede construir el siguiente sistema:
. Con esta definición se puede construir el siguiente sistema:
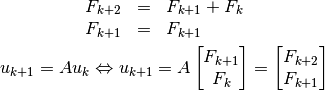
por lo tanto 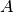 es:
es:
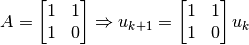
Si se calculan los valores y vectores propios:
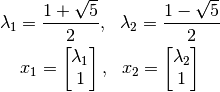
Recapitulando, si se usa la ecuación 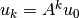 :
:
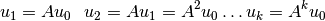
para encontrar 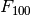 :
:
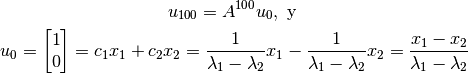
por lo tanto,
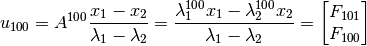
Interesa el segundo componente de 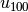 :
:
![u_{100}=& \begin{bmatrix} \frac{\lambda_{1}^{100} x_1}{\lambda_1 - \lambda_2} - \frac{\lambda_{2}^{100} x_2}{\lambda_1 - \lambda_2} \end{bmatrix} \\
=& \ldots \rightarrow F_{100} = \frac{1}{\sqrt{5}} \left[\left( \frac{1 + \sqrt{5}}{2} \right)^{100} - \left( \frac{1 - \sqrt{5}}{2} \right)^{100}\right] \approx 3,54 \times 10^{20}](_images/math/b85853bba2f36de7dee8760c61e36cd19ebd50de.png)
Factorizaciones que Revelan Valores Propios¶
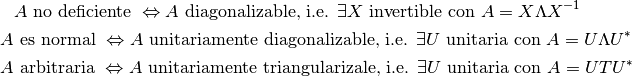
Nota
Sea 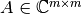 una matriz normal, es decir,
una matriz normal, es decir, 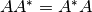 , donde
, donde 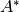 denota la matriz hermitiana adjunta de
denota la matriz hermitiana adjunta de 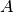 .
.
Las matrices normales poseen un sistema completo de valores y vectores propios, es decir, tienen 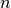 valores propios
valores propios 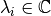 , a cada valor propio
, a cada valor propio 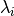 le corresponde exactamente un vector propio
le corresponde exactamente un vector propio 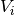 , y el sistema de los
, y el sistema de los 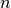 vectores propios es un sistema ortogonal completo, i.e., constituye una base ortogonal de
vectores propios es un sistema ortogonal completo, i.e., constituye una base ortogonal de 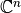 .
.
Teorema de Gerschgorin¶
El teorema de Gerschgorin es un resultado muy útil que permite estimar bastante bien los valores propios de una matriz simétrica o no simétrica.
Teorema:
Sea ![A=[a_{ij}] \in C^{n \times n}](_images/math/91ab372db22ca63a8c539adf18b98494eedf9a17.png) , una matriz cualquiera. Entonces todo valor propio de
, una matriz cualquiera. Entonces todo valor propio de 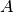 está en a lo menos un disco del plano complejo
está en a lo menos un disco del plano complejo 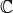 centrado en
centrado en 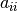 y con radio
y con radio 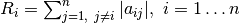 :
:
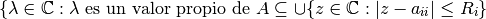
Además, Si 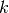 de estos
de estos 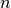 discos forman un dominio conexo disjunto de los restantes
discos forman un dominio conexo disjunto de los restantes 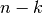 discos, entonces hay precisamente
discos, entonces hay precisamente 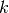 valores propios en ese dominio conexo.
valores propios en ese dominio conexo.
Nota
Un dominio es conexo si cualquier par de puntos en el dominio puede ser conectado por una curva que está completamente contenida en el dominio.
Ejemplo Para 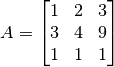
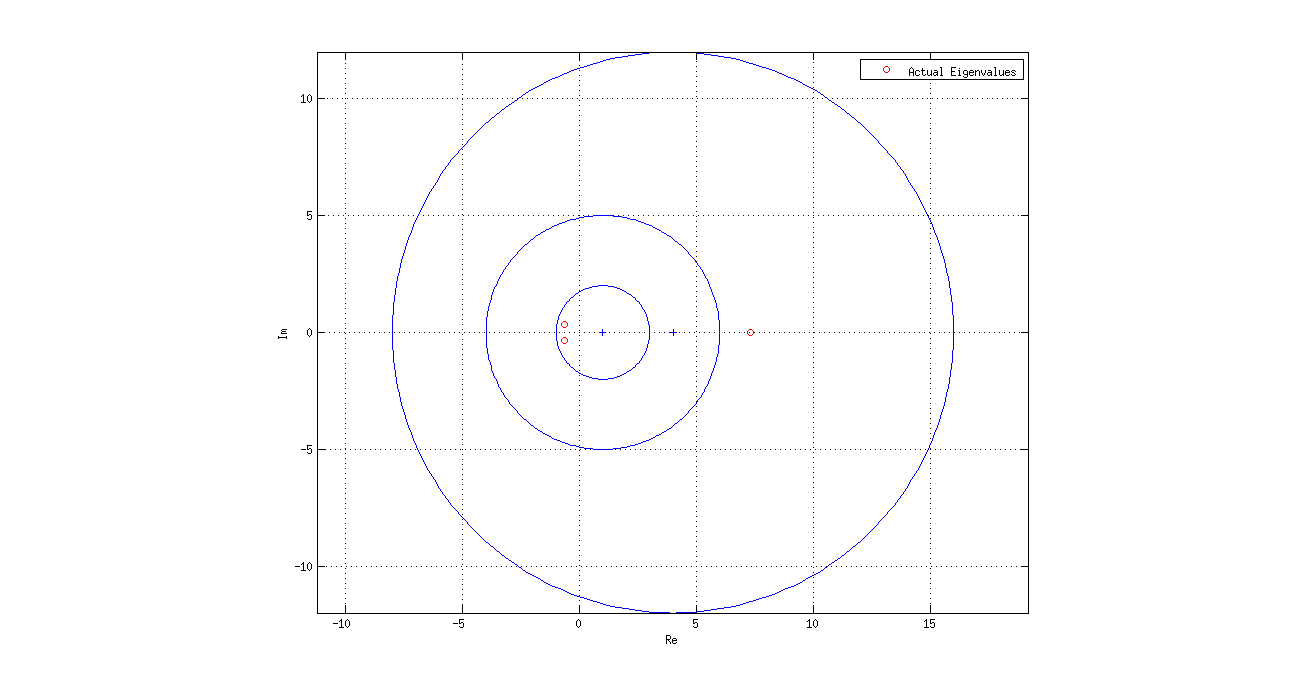
Demostración¶
Sea 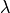 un valor propio de
un valor propio de 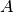 y
y 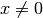 su correspondiente vector propio, i.e.,
su correspondiente vector propio, i.e., 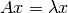 .
.
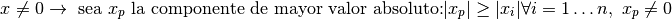
Entonces la p-ésima ecuación del sistema 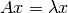 se puede escribir de la forma:
se puede escribir de la forma:
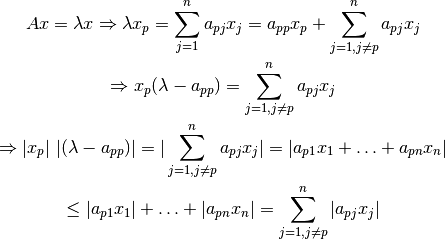
por lo tanto:
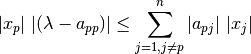
y si dividimos por 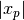 y utilizamos la consideración
y utilizamos la consideración 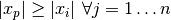 :
:
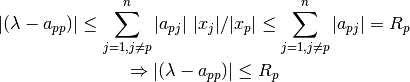
Luego 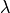 está contenido en el disco
está contenido en el disco 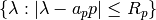 .
.
Ejercicio en Clases 1.3¶
- Sea
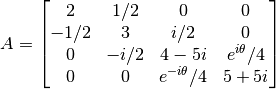 .
Determinar gráficamente los valores propios.
.
Determinar gráficamente los valores propios.
Se debe calcular los centros y radios de los discos de Gerschgorin:
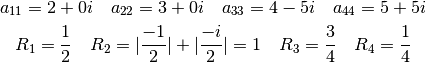
Ejercicio Propuesto¶
- Sea
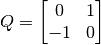 una matriz de rotación. Calcular valores y vectores propios y explicar claramente que ocurre en esta situación. Hint: Revisar Ejemplo 5, Capítulo 6: Eigenvalues and Eigenvectors, del libro “Introduction to Linear Algebra”, Gilbert Strang, Fourth Edition.
una matriz de rotación. Calcular valores y vectores propios y explicar claramente que ocurre en esta situación. Hint: Revisar Ejemplo 5, Capítulo 6: Eigenvalues and Eigenvectors, del libro “Introduction to Linear Algebra”, Gilbert Strang, Fourth Edition.
