Clase 10: Splines¶
Bibliografía de la Clase:
- Introduction to Numerical Analysis - J.Stoer, R.Bulirsch. Chapter 2: Interpolation.
- Guía profesor Luis Salinas
Splines cúbicos¶
Las funciones splines permiten obtener curvas que tienden a exhibir menos oscilaciones que los polinomios de alto grado.
Si se tiene un conjunto de datos  , la
idea de los splines es ajustar un polinomio de grado
, la
idea de los splines es ajustar un polinomio de grado 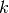 en cada
intervalo de la partición equiespaciada de
en cada
intervalo de la partición equiespaciada de  datos:
datos:

Por lo tanto, es posible encontrar 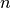 funciones splines
funciones splines  que ajusten los intervalos
que ajusten los intervalos ![[x_j,x_{j+1}]](_images/math/ac643df9e1e4041af2044205f55607ba0ffa646f.png) .
.
La siguiente figura muestra diferentes funciones splines:
(Source code, png, hires.png, pdf)

En el caso particular de que estas funciones sean cúbicas (i.e  )
son conocidas como splines cúbicos.
)
son conocidas como splines cúbicos.
Splines Cúbicos
Un spline cúbico ![S:[a,b] \to \mathbb{R}](_images/math/d4b654e2ef2c17c06090bde02efc211c9eb3f2e7.png) es una función en el intervalo
es una función en el intervalo ![[a,b]](_images/math/8ecbd1ba3da8f2adef66a63f2ab32c47e63fa734.png) que tiene las siguientes
propiedades:
que tiene las siguientes
propiedades:
- Dos veces continuamente diferenciable en el intervalo [a,b]
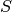 coincide en cada subintervalo
coincide en cada subintervalo ![[x_j,x_{j+1}], \quad j=0,\dots n-1](_images/math/c3164984b12914dac07b33d0e0040ebb381e89ff.png) con un polinomio de grado 3
con un polinomio de grado 3  .
.
Por lo tanto, los splines cúbicos son polinomios cúbicos  unidos de
manera que sus valores
unidos de
manera que sus valores  y sus dos primeras derivadas coinciden en los
puntos de apoyo
y sus dos primeras derivadas coinciden en los
puntos de apoyo  (ver figura 1).
(ver figura 1).
Los splines cúbicos  y sus respectivas derivadas son de la forma:
y sus respectivas derivadas son de la forma:
(1)
(2)
(3)
Ya que la data se asume equiespaciada, se definirá además:
(4)
Para poder encontrar el polinomio interpolador  es necesario
encontrar todos los coeficientes
es necesario
encontrar todos los coeficientes  y
y  . Para esto se
utilizarán las relaciones que provienen de las propiedades de los
splines cúbicos
. Para esto se
utilizarán las relaciones que provienen de las propiedades de los
splines cúbicos  definidos previamente:
definidos previamente:
1) Interpolación en  ¶
¶

De la ecuación (1) se tiene que:
(5)
Por lo tanto los valores de  se calculan de manera directa.
se calculan de manera directa.
3) Continuidad de 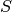 en
en  ¶
¶

Usando las ecuaciones (1) y (4) se tiene que:

Ahora usando la ecuación (6) para  :
:

(7)
4) Continuidad de la primera derivada¶

Usando las ecuaciones (2) y (4):

Ahora usando la ecuación (6) para  :
:

Si reemplazamos la ecuación (7) en esta expresión se obtiene el siguiente sistema:

(8)
5) Condiciones de borde¶
Debido a que el sistema presentado en la ecuación (8) sólo
tiene  ecuaciones, se necesita definir condiciones de borde para
los casos
ecuaciones, se necesita definir condiciones de borde para
los casos  y
y  . Se tienen dos tipos de condiciones de borde:
. Se tienen dos tipos de condiciones de borde:
- Frontera libre o natural

Si aplicamos la ecuación (3) se tiene que:

- Frontera fija

En general, las condiciones de frontera fija son más precisas que las de frontera libre, pero necesitan información acerca de las derivadas en los bordes.
Ejercicio propuesto
Demuestre que para la condición de frontera fija se cumple que  y que:
y que:

Búsqueda de coeficientes¶
Luego de obtener las expresiones dadas las restricciones de las funciones splines, lo que queda es ir obteniendo los coeficientes de los polinomios.
De la ecuación (8) se obtienen  ecuaciones lineales que
pueden expresarse matricialmente como:
ecuaciones lineales que
pueden expresarse matricialmente como:

De este sistema de ecuaciones se obtienen los coeficientes  que
permiten obtener los coficientes
que
permiten obtener los coficientes  (ecuación (7)) y los
(ecuación (7)) y los  (ecuación (6)). Recordar que los
(ecuación (6)). Recordar que los  están determinados por los
valores
están determinados por los
valores  .
.
Ejercicio en clases
Usando fronter libre determine el spline cúbico 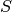 que interpola la data
que interpola la data

Ejercicio propuesto
Un spline cúbico 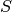 definido en el intervalor [0,2] se define como:
definido en el intervalor [0,2] se define como:

Determine los coeficientes  ,
,  y
y  considerando condiciones de
frontera libre.
considerando condiciones de
frontera libre.




