Clase 11: Integración Numérica¶
Bibliografía de la Clase:
- Numerical Analysis - Richard L. Burden, J. Douglas Faires. Capítulo 3 y Capítulo 4.
Polinomios de Lagrange¶
Idea. El problema de determinar un polinomio de grado uno que pase por los puntos  y
y  , es lo mismo que aproximar una función
, es lo mismo que aproximar una función  , en la cual
, en la cual  y
y  .
.
Primero se definen las funciones:

y se define el polinomio:

Además:

y se obtiene:

Por lo tanto  es una función lineal única que pasa por los puntos
es una función lineal única que pasa por los puntos  y
y  .
.
La generalización de la interpolación lineal, considera la construcción de un polinomio de grado a lo más 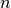 que pasa por los
que pasa por los  puntos:
puntos:

Teorema: Polinomio Interpolador de Lagrange
Si  son
son  números distintos y
números distintos y  es una función cuyos valores están dados para tales puntos, entonces el polinomio
es una función cuyos valores están dados para tales puntos, entonces el polinomio  único y de grado a lo más
único y de grado a lo más 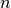 existe y:
existe y:

Teorema: Polinomio Interpolador de Lagrange y Error:
Si  son
son  números distintos en el intervalo
números distintos en el intervalo ![[a,b]](_images/math/8ecbd1ba3da8f2adef66a63f2ab32c47e63fa734.png) y
y ![f \in C^{n+1}[a,b]](_images/math/25f10cf4e0ac17c358bc99bb36ba845ffbc56ab3.png) , entonces,
, entonces, ![\forall x \in [a,b]](_images/math/372a7d06de69343d51472f7b57613c9838476663.png) , existe un número
, existe un número ![\xi (x) \in [a,b]](_images/math/5dfd04eceba866e7041abfa174d2fba5311e077d.png) tal que:
tal que:

(Revisar clase Error en la interpolación polinomial )
Nota
El uso de esta fórmula del error se limita a las funciones cuyas derivadas tienen cotas conocidas.
Ejemplo¶
Usando los números (o nodos)  , y
, y  encontrar el polinomio interpolador de segundo orden para
encontrar el polinomio interpolador de segundo orden para  .
.
Integración Numérica¶
En algunas aplicaciones es necesario evaluar una integral definida de una función que no tiene una antiderivada explícita o fácil de obtener. La cuadratura numérica es el método más simple para aproximar  y consiste en usar una sumatoria para aproximar la integral:
y consiste en usar una sumatoria para aproximar la integral:

Los métodos de cuadratura numérica utilizados se basan en la integración de polinomios interpoladores, para lo cual, se realizan los siguientes pasos:
- Seleccionar un conjunto de nodos
 sobre el intervalo
sobre el intervalo ![[a,b]](_images/math/8ecbd1ba3da8f2adef66a63f2ab32c47e63fa734.png)
- Integrar un polinomio interpolador sobre el mismo intervalo, por ejemplo un polinomio integrador de Lagrange:

- Calcular su término de error de truncamiento en
![[a,b]](_images/math/8ecbd1ba3da8f2adef66a63f2ab32c47e63fa734.png) para obtener
para obtener

- donde
![(\xi (x)) \in [a,b]](_images/math/8483cc95551a6465f077fe6d9da6d21aa38dfcf0.png) para cada
para cada 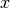 , y:
, y:

- Por lo tanto, la fórmula de cuadratura es:

- con un error

La metodología explicada, para Polinomios de Lagrange de de primer y segundo orden, con nodos igualmente espaciados da origen a la Regla del Trapecio y Regla de Simpson.
Regla del Trapecio¶
Es llamada la regla del trapecio porque cuando la función  es una función con valores positivos,
es una función con valores positivos,  es aproximadamente
el área del trapecio, como lo muestra la sgte. figura:
es aproximadamente
el área del trapecio, como lo muestra la sgte. figura:

Fig. 1. Fuente: http://en.wikipedia.org/wiki/Trapezoidal_rule.
Si se utiliza el polinomio de Lagrange de grado  :
:

Se obtiene la regla del trapecio, para  :
:

Nota
¿Para qué tipo de funciones se puede saber inmediatamente que la integración es exacta?
Desarrollo¶

con  , y
, y  se obtiene:
se obtiene:
![\begin{array}{lll}
\int_a^b f(x)dx & = & \int_{x_0}^{x_1} P_1 (x) dx + \int_{x_0}^{x_1} E_1(f)dx \\
& & \\
& = &\int_{x_0}^{x_1} \left [ \frac{(x-x_1)}{(x_0-x_1)} f(x_0) + \frac{(x-x_0)}{(x_1-x_0)} f(x_1) \right ] + \int_{x_0}^{x_1} E_1(f)dx \\
& & \\
& = & \left [ \frac{(x-x_1)^2}{2(x_0-x_1)} f(x_0) + \frac{(x-x_0)^2}{2(x_1-x_0)} f(x_1) \right ]_{x_0}^{x_1} + \int_{x_0}^{x_1} E_1(f)dx\\
& & \\
& = & \left [ \frac{(x_1-x_0)^2}{2(x_1-x_0)} f(x_1) - \frac{(x_0-x_1)^2}{2(x_0-x_1)} f(x_0) \right ]_{x_0}^{x_1} + \int_{x_0}^{x_1} E_1(f)dx\\
& & \\
& = & \frac{h}{2} (f(x_0) + f(x_1)) + \int_{x_0}^{x_1} E_1(f)dx\\
\end{array}](_images/math/1496eebc66c926bb767b1f8352aafcfa2be40d8a.png)
Se calcula el error de integración, aplicando el teorema del valor medio para algún ![\xi \in [a,b]](_images/math/7fecd4f6521e366aa9b46ea2c4aee9b315d35692.png) :
:
![\begin{array}{lll}
\int_{x_0}^{x_1} E_1(f)dx &= & \frac{1}{2}\int_{x_0}^{x_1} (x-x_0) (x-x_1)f''(\xi)dx\\
& & \\
& = & \frac{f''(\xi)}{2} \int_{x_0}^{x_1} [x^2 - (x_0 + x_1)x + x_0 x_1]dx \\
& & \\
&= & \frac{f''(\xi)}{2} \left [ \frac{x^3}{3} - (x_0 + x_1)\frac{x^2}{2} + (x_0 x_1)x \right]_{x_0}^{x_1}\\
& & \\
&= & \frac{f''(\xi)}{12} (x^3_1 - 3 x_0 x_1^2 + 3 x_0^2 x_1 - x_0^3)\\
& & \\
& = & \frac{f''(\xi)}{12} (x_1 - x_0)^3 \\
& & \\
& = & - \frac{h^3}{12}f''(\xi) \\
\end{array}](_images/math/22785dc529dd76c1819c0621721d3b36eeb20425.png)
Ejercicio¶
Usando la regla del trapecio, calcular la integral  , considerando que su valor exacto con ocho cifras decimales es 0,74682413.
, considerando que su valor exacto con ocho cifras decimales es 0,74682413.
Regla de Simpson¶
La regla de Simpson aparece al integrar sobre el intervalo ![[a,b]](_images/math/8ecbd1ba3da8f2adef66a63f2ab32c47e63fa734.png) utilizando el segundo polinomio de Lagrange, con nodos:
utilizando el segundo polinomio de Lagrange, con nodos:  , y
, y  :
:

Fig. 2. Fuente: http://en.wikipedia.org/wiki/Simpson’s_rule
y corresponde a:
![\int_{x_0}^{x_2} f(x) dx = \frac{h}{3} [f(x_0) + 4 f(x_1) +f (x_2)] - \frac{h^5}{90}f^{(4)}(\xi)](_images/math/9c87a7371a491baa9a9d498bda98b9dcf2181a69.png)
Nota
¿Para qué tipo de funciones se puede saber inmediatamente que la integración es exacta?
Para llegar a la regla de Simpson:

Pero esta expresión, solamente permite obtener un error de integración  . Aproximando la función
. Aproximando la función  mediante un polinomio de Taylor de tercer orden alrededor de
mediante un polinomio de Taylor de tercer orden alrededor de  , se obtiene una mejor precisión.
, se obtiene una mejor precisión.
Recordar: Teorema de Taylor.
Sea  un entero y se la función
un entero y se la función 
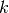 veces diferenciable en el punto
veces diferenciable en el punto  . Entonces existe una función
. Entonces existe una función  tal que:
tal que:

Ejercicio¶
Usando la regla de Simpson, calcular la integral  , considerando que su valor exacto con ocho cifras decimales es 0,74682413.
, considerando que su valor exacto con ocho cifras decimales es 0,74682413.
Nota
La regla del trapecio y la regla de Simpson son ejemplos de una clase de métodos conocida como fórmulas de Newton - Cotes. Existen dos tipos de fórmulas Newton - Cotes: abiertas y cerradas. La fórmula cerrada utiliza puntos equiespaciados,  , y se denomina cerrada porque incluye los límites del intervalo
, y se denomina cerrada porque incluye los límites del intervalo ![[a,b]](_images/math/8ecbd1ba3da8f2adef66a63f2ab32c47e63fa734.png) como puntos de apoyo.
como puntos de apoyo.
Ejercicios Propuestos¶
- Demostrar que el polinomio interpolador de Lagrange es único.
- Obtener la Regla del Trapecio, utilizando el polinomio de Taylor de tercer orden. Hint: Ver Capítulo 4.3 Elements of Numerical Integration, Numerical Analysis de Burden.
