Clase 9: L’Hermite y Cotas para el error¶
Bibliografía de la Clase:
- Guía profesor Luis Salinas
- Guía profesor Roberto León
- Introduction to Numerical Analysis - J.Stoer, R.Bulirsch
- Análisis Numérico - Richard L. Burden - J. Douglas Faires
L’Hermite¶
El método visto previamante (Diferencias divididas de newton) resulta de manera óptima para la búsqueda de un polinomio interpolador, para una cierta data  .
Pero no siempre la data está compuesta solo de puntos de apoyo, es decir, la data puede ser enriquecida con más información, que el método de Newton no puede
aprovechar.
.
Pero no siempre la data está compuesta solo de puntos de apoyo, es decir, la data puede ser enriquecida con más información, que el método de Newton no puede
aprovechar.
Para la interpolación de L’Hermite se considera con información que ayudará a obtener mayor precisión en la interpolación: data  y además datos
sobre las derivadas
y además datos
sobre las derivadas  . En este caso, los grados de los polinomios cambian: antes eran
. En este caso, los grados de los polinomios cambian: antes eran  datos interpolados por un polinomio de grado
datos interpolados por un polinomio de grado 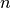 , en este caso
el grado del polinomio en base a la cantidad de datos de puntos de apoyo y derivadas.
, en este caso
el grado del polinomio en base a la cantidad de datos de puntos de apoyo y derivadas.
Supongamos que se tiene la siguiente data:  ,
,  ,
,  ,
,  ,
,  . Si se cuenta la cantidad de datos,
se tienen: 5 datos, lo cual implica que deberá construirse un polinomio de grado 4. El polinomio tendrá por ende 5 coeficientes
. Si se cuenta la cantidad de datos,
se tienen: 5 datos, lo cual implica que deberá construirse un polinomio de grado 4. El polinomio tendrá por ende 5 coeficientes  y tendra la siguiente forma:
y tendra la siguiente forma:

La razón de que el polinomio tenga esa forma, es la misma que la realizada para la interpolación mediante diferencias dividades ( debe ser raíz del
debe ser raíz del  ), pero
el factor
), pero
el factor  se repite con relación a la cantidad derivadas, por ejemplo para
se repite con relación a la cantidad derivadas, por ejemplo para  se tiene una derivada, por lo tanto se repite 1 veces, y su razón es porque
si se deriva este polinomio, y se evalúa en
se tiene una derivada, por lo tanto se repite 1 veces, y su razón es porque
si se deriva este polinomio, y se evalúa en  da el coeficiente
da el coeficiente  :
:

Proceso similar ocurre para  . Pero en la forma de Newton no se considera el último factor, recordar que para
. Pero en la forma de Newton no se considera el último factor, recordar que para 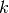 puntos solo se llegaba hasta el
puntos solo se llegaba hasta el  .
La idea de esta expresión es asociar cada
.
La idea de esta expresión es asociar cada  a la data de la ordenada o derivada.
a la data de la ordenada o derivada.
Pregunta ¿Se puede aplicar la técnica de diferencias divididas?.
Respuesta, la técnica tal cual no puede aplicarse, debido a que en el cuadro esquemático se hacía la diferencia entre  y
y  , y en este caso se tiene
un
, y en este caso se tiene
un  asociado a más de un par, por lo que inminentemente se realizarán denominadores
asociado a más de un par, por lo que inminentemente se realizarán denominadores  . Por lo que es necesario modificar la técnica de diferencias
divididas.
. Por lo que es necesario modificar la técnica de diferencias
divididas.
El caso problemático entonces es ![f[x_i, x_i, \ldots, x_i]](_images/math/dce9843145e27ac77adcc405fd15fda391d14623.png) , si para esa abscisa
, si para esa abscisa  se repite
se repite 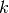 veces entonces:
veces entonces:
![f[x_i, x_i, \ldots, x_i] = \frac{f_i^k}{k!}](_images/math/e134a69e6ba011fec9bbddaacc8b38a46731d496.png)
y el nuevo cuadro esquemático queda de la siguiente forma:
Error en la interpolación polinomial¶
Nuevamente se considera una función  de la cual se tiene una data
de la cual se tiene una data  , la cual se interpola con un polinomio que
llamaremos
, la cual se interpola con un polinomio que
llamaremos  . Es conocido que el polinomio pasa exactamente por lo puntos de la data, es decir:
. Es conocido que el polinomio pasa exactamente por lo puntos de la data, es decir:

Lo que se busca estimar para este caso, es la diferencia entre  para los
para los  .
.
Teorema
Si la función  tiene una (n+1) derivada, es decir
tiene una (n+1) derivada, es decir  , entonces para todos los
, entonces para todos los  existe un número
existe un número  perteneciente
al intervalo más pequeño
perteneciente
al intervalo más pequeño ![I[x_0, \ldots, x_n, \bar{x}]](_images/math/21a3b019ae0e2bb372ce1275d9a35e975d826de0.png) que contiene
que contiene  y los puntos de soporte
y los puntos de soporte  tal que:
tal que:

donde:

Demostración¶
Suponga entonces que el polinomio  corresponde a la interpolación polinomial de la función
corresponde a la interpolación polinomial de la función  en la data
en la data  , además
suponga que
, además
suponga que  . Lo que se busca entonces es encontrar una constante
. Lo que se busca entonces es encontrar una constante  tal que:
tal que:

Para los  se cumplirá que:
se cumplirá que:

Ahora fijándose en las raíces del polinomio  , se tienen las raices
, se tienen las raices  y además la
y además la  , en total
, en total  raíces.
Recordar que si un polinomio tiene
raíces.
Recordar que si un polinomio tiene  raíces, entonces su derivada, tendrá al menos
raíces, entonces su derivada, tendrá al menos  raíces. Además
raíces. Además  , ya que
, ya que  tiene grado
tiene grado 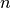 . Entonces:
. Entonces:

Ejercicio en Clase 9.2¶
Si  y se tiene la data
y se tiene la data  para
para  Encuentre una cota para el error.
Encuentre una cota para el error.
Desarrollo¶





