Clase 12: Más Sobre Integración Numérica¶

Bibliografía de la Clase:

Introduction to Numerical Analysis - J.Stoer, R.Bulirsch. Chapter
Guía profesor Luis Salinas

Regla del Trapecio Compuesto¶

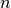Es posible obtener una mejor aproximación de la integral $\int_a^b f(x) dx$ si el intervalo $[a,b]$ es subidividido en $n$ subintervalos y se aplica una regla de integración para cada uno de los intervalos, como lo muestra la siguiente figura.

Si se aplica la regla del trapecio a cada uno de los intervalos con $h=\frac{(b-a)}{n}$ y $x_i = a + ih$ para cada $i=0, \ldots , n$ , se tiene:

$\begin{array}{lll} \int_a^b f(x) dx &= & \sum\limits_{i=0}^{n-1} \frac{h}{2} [ f(x_i) + f(x_{i+1}) ] - \frac{h^3}{12}f''(\xi)\\ & & \\ &= & \frac{h}{2} \left [ f(x_0) + 2 \sum\limits_{i=1}^{n-1} f(x_i) + f_{x_n} \right ] - \sum\limits_{i=1}^{n-1} \frac{h^3}{12}f''(\xi) \\ & & \\ &= & \frac{h}{2} \left [ f(x_0) + 2 \sum\limits_{i=1}^{n-1} f(x_i) + f_{x_n} \right ] - \frac{(b-a)h^2}{12}f''(\xi) \\ \end{array}$

Ejercicio¶

Usar la regla del trapecio compuesto para estimar $\int\limits_{1}^{5} \sqrt{1+x^2}$ , con $n=8$ .

Regla de Simpson Compuesto¶

Si se aplica la regla de Simpson para cada uno de los subintervalos se obtiene:

$\begin{array}{lll} \int_a^b f(x) d(x) &= & \sum\limits_{i=0}^{n-2} \frac{h}{3} [ f(x_i) + 4 f(x_{i+1})+ f(x_{i+2}) ] - \frac{h^5}{90} f^{(4)}(\xi) \\ & &\\ &= & \frac{h}{3} \left [ f(x_0) + 4 \sum\limits_{i=1}^{\frac{n}{2}} f (x_{2i-1}) +2 \sum\limits_{i=1}^{\frac{n}{2}-1} f (x_{2i}) + f (x_n) \right ] - \sum\limits_{i=1}^{\frac{n}{2}} \frac{h^5}{90}f^{(4)}(\xi)\\ & &\\ &= & \frac{h}{3} \left [ f(x_0) + 4 \sum\limits_{i=1}^{\frac{n}{2}} f (x_{2i-1}) +2 \sum\limits_{i=1}^{\frac{n}{2}-1} f (x_{2i}) + f(x_n) \right ] - \frac{(b-a)h^4}{180}f^{(4)}(\xi)\\ \end{array}$

Ejercicio¶

Usar la regla de Simpson compuesto para estimar $\int\limits_{1}^{4} \sqrt{1+x^3}$ , con $n=6$ .

Cuadratura de Gauss¶

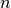Las fórmulas vistas hasta el momento utiliza valores de la función $f$ para puntos igualmente espaciados, y la fórmula es exacta al menos para polinomios de grado $n$ (¿por qué?). Considerar las situaciones mostradas en la siguiente figura:

La regla del Trapecio aproxima la integral mediante una función lineal que une los puntos extremos de la función. Pero se ve que no es una buena aproximación. Considerar la nueva situación que muestra la figura:

La cuadratura de Gauss escoge los puntos donde el error es mínimo. Los puntos de apoyo $x_1,x_2, \ldots , x_n$ en el intervalo $[a,b]$ y los coeficientes $c_1, c_2, \ldots , c_n$ son escogidos para minimizar el error, y hace posible que la fórmula sea exacta para polinomio de grado $2n-1$ si se escogen los puntos de manera apropiada, y no igualmente separados.

$\int\limits_{a}^{b} \omega (x) f(x) dx \approx \sum\limits_{i=1}^{n}c_if(x_i)$

donde $\omega (x) \geq 0$ es una función de ponderación dada sobre el intervalo $[a,b]$

Para entender como funciona la cuadratura de Gauss, primero se discutirá brevemente el concepto de conjunto ortogonal de funciones.

Funciones ortogonales

El conjunto de funciones $\phi_0 (x), \phi_1 (x), \ldots , \phi_n (x)$ , es un conjunto ortogonal en $[a,b]$ con respecto a la función de peso $v(x)$ si y solo si:

$\int\limits_{a}^{b} v(x) \phi_i (x) \phi_j (x) dx = \delta_{ij} \ \ \ 0 \leq i, j \leq n$

Polinomios de Legendre

Los polinomios de Legendre pueden generarse en forma recursiva:

$\begin{array}{lll} P_0 (x) &= & 1 \\ & & \\ P_1(x) & = & x \\ & & \\ P_{n+1}(x) & = &\frac{(2n+1)xP_n (x) - n P_{n-1}(x)}{n+1}\\ \end{array}$

Puede verificarse fácilmente que estos polinomios son ortogonales en el intervalo $[-1,1]$ con respecto a la función de peso $v(x)=1$ .

Las raíces de los polinomios de Legendre son los puntos de apoyo en los cuales se evalúa la función $f$ , para el procedimiento de la cuadratura de Gauss. Por otro, las constantes $c_i$ se obtienen mediante:

$c_i = \int\limits_{-1}^{1} \prod\limits_{j=1, j\neq i }^{n} \frac{x-x_j}{x_i-x_j}dx$

Ejemplo¶

Si se considera el polinomio de Legendre $P_2(x)=x^2 - \frac{1}{3}$ , las raíces del polinomio son:

$P_2(x) =x^2 - \frac{1}{3} = 0 x^2 = \frac{1}{3} \Rightarrow x_1=-\frac{\sqrt{3}}{3}, \ x_2=\frac{\sqrt{3}}{3}$

Luego se debe calcular $c_1$ y $c_2$ :

$c_1 = \int\limits_{-1}^{1} \frac{x-x_2}{x_1 - x_2}dx = \int\limits_{-1}^{1} \frac{x- \frac{\sqrt{3}}{3}}{-\frac{2\sqrt{3}}{3}}dx = -\frac{3}{2\sqrt{3}} \left [ \frac{x^2}{2} - \frac{\sqrt{3}x}{3} \right]_{-1}^{1}$

de forma similar se obtiene $c_2= \frac{3}{2\sqrt{3}} \left [ \frac{x^2}{2} + \frac{\sqrt{3}x}{3} \right]_{-1}^{1}$ , y finalmente la cuadratura de Gauss-Legendre para $n=2$ :

$\int\limits_{-1}^{1} f(x) dx \approx 1\times f(\frac{-\sqrt{3}}{3}) + 1\times f(\frac{\sqrt{3}}{3})$

Teorema¶

Suponer $x_1, x_2, \ldots , x_n$ son las raíces del polinomio de Legendre $P_n (x)$ de n-ésimo grado y que para cada $i=1, \ldots , n$ , los números $c_i$ están definidos por:

$c_i = \int\limits_{-1}^{1} \prod\limits_{j=1, j\neq i }^{n} \frac{x-x_j}{x_i-x_j}dx$

Si $P(x)$ es un polinomio cualquiera de un grado menor que 2n, entonces:

$\int\limits_{-1}^{1} P(x)dx = \sum\limits_{i=1}^{n}c_i P(x_i)$

Es decir se obtiene una aproximación exacta utilizando los nodos $x_1, \ldots , x_n$ correspondientes a las raíces del polinomio de Legendre de grado $n$ .

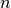Ejercicios Propuestos¶

1. Verificar que los polinomios de Legendre son ortogonales en el intervalo $[-1,1]$ con respecto a la función de peso $v(x)=1$ .

Clase 12: Más Sobre Integración Numérica¶

Regla del Trapecio Compuesto¶

Ejercicio¶

Regla de Simpson Compuesto¶

Ejercicio¶

Cuadratura de Gauss¶

Ejemplo¶

Teorema¶

Ejercicios Propuestos¶

Contenidos

Tema anterior

Próximo tema

Esta página

Navegación

Clase 12: Más Sobre Integración Numérica¶

Regla del Trapecio Compuesto¶

Ejercicio¶

Regla de Simpson Compuesto¶

Ejercicio¶

Cuadratura de Gauss¶

Ejemplo¶

Teorema¶

Ejercicios Propuestos¶

Contenidos

Tema anterior

Próximo tema

Esta página

Búsqueda rápida

Navegación