Clase 13: Ecuaciones Diferenciales Ordinarias I¶

Bibliografía de la Clase:

Introduction to Numerical Analysis - J.Stoer, R.Bulirsch. Chapter 7: Ordinary Differential Equations
Métodos Numéricos para Ingenieros. S. Chapra, R.Canale. Capítulo 25: Métodos de Runge-Kutta
Guía profesor Luis Salinas

Introdución: Ecuaciones Diferenciales¶

Una ecuación diferencial es una ecuación que contiene una función desconocida y sus derivadas.

Ejemplos de ecuaciones diferenciales son:

$\frac{dy}{dx} = 5x + 3, \ \ \ \ \ e^{y} \frac{dy^2}{dx^2} + 2 \left ( \frac{dy}{dx} \right )^{2} = 1, \ \ \ \ \ \dfrac{\partial^2 y}{\partial t^2} - 4 \dfrac{\partial^2 y}{\partial x^2} = 0$

Una ecuación diferencial es una ecuación diferencial ordinaria (EDO) si la función desconocida depende solamente de una variable. Si la función desconocida depende de dos o más variables, la ecuación diferencial se denomina ecuación diferencial parcial (EDP).

El orden de una ecuación diferencial es el mayor orden de la derivada que aparece en la ecuación.

Problemas de Valor Inicial¶

Las ecuaciones diferenciales permiten modelar problemas de ciencia e ingeniería, y una parte importante de ellos requiere resolver un problema de valor inicial, es decir, se debe resolver una ecuación diferencial que satisface una condición inicial dada.

Idea:

Se busca una solución $y$ de $y'=f(x,y)$ para un $x_0$ e $y_0$ dados, que satisfacen la condición: $y(x_0)=y_0$ .

También se puede considerar un sistema de 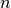$n$ EDOs:

$y'_1(x)=f_1(x,y_1(x), \ldots , y_n(x)), y'_2(x)=f_2(x,y_1(x), \ldots , y_n(x)) \ldots y'_n(x)=f_n(x,y_1(x), \ldots , y_n(x))$

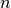de $n$ ecuaciones reales desconocidas $y_i(x), i=1 \ldots n$ , de variables reales. Estos sistemas se escriben de forma vectorial:

(1) ${\bf y}'(x)= {\bf f}(x,{\bf y}) = \begin{bmatrix}y'_1 \\ \vdots \\ y'_n\end{bmatrix}, \ \ {\bf f}(x,{\bf y})=\begin{bmatrix}f_1(x,y_1(x), \ldots , y_n(x)) \\ \vdots \\ f_n(x,y_1(x), \ldots , y_n(x)) \end{bmatrix}, \ \ {\bf y}(x_0)= {\bf y}_0 = \begin{bmatrix}y_{10} \\ \vdots \\ y_{n0}\end{bmatrix}$

Nota

Las ecuaciones diferenciales ordinarias de orden superior pueden ser reducidas a sistemas de ecuaciones, como veremos en el ejercicio 1.2.

Método de Euler¶

Un primer método numérico para la solución del problema de valor inicial:

(2) $y' = f(x,y), \ \ y(x_0)=y_0$

Se considera que $f(x,y(x))$ es simplemente la pendiente $y'(x)$ de la solución deseada $y(x)$ del problema (2). Se tiene que para $h\neq 0$ y una suceción equiespaciada de abscisas $x_k$ con $x_{k+1} = x_k + h, k \in \mathbb{N}_0$ :

(3) $\frac{y(x_{k+1}) - y(x_k)}{h} \approx f(x_k,y(x_k)) \ \ \ \equiv \ \ \ y(x_{k+1}) \approx y(x_k) + h f(x_k,y(x_k))$

Notar que $y(x)$ denota la solución exacta de (2), y la ecuación (3) sugiere la ecuación de recurrencias:

(4) $\frac{y_{k+1} - y_k}{h} = f(x_k,y_k), \ \ k \in \mathbb{N}_0, \ \ \text{ con } y_0=y(x_0)=\text{dato}$

equivalente a:

(5) $y_{k+1} = y_k + h f(x_k,y_k)), \ \ k \in \mathbb{N}_0, \ \ \text{ con } y_0=y(x_0)=\text{dato}$

Nota

Solamente se puede esperar que $y_k$ sea aproximadamente igual a $y(x_k)$ , i.e., $y_k \approx y(x_k)$ . No obstante, la ecuación (4) permite, en muchos casos, obtener una solución numérica razonable del problema de valor inicial.

Ejercicio 1¶

1.1. Para soltar la mano: utilizando el método de Euler resolver el problema de valor inicial:

$y' = y - t^2 + 1, \ \ 0 \leq t \leq 2, \ \ y(0) = 0,5$

con $N=10 \rightarrow h = \frac{2}{10}=0,2$ , $t_k=0.2 k, y_0=0.5$ (la solución exacta es $y(t)= (t+1)^2 - 0,5 e^t$ ).

1.2. Las oscilaciones de un péndulo con excitación $\varphi(t)$ y amortiguamiento proporcional a la velocidad instantánea de oscilación, vienen modelada por el problema de valores iniciales:

$\ddot{\vartheta}(t) + \kappa\,\dot{\vartheta}(t) + \mu\,\sin\vartheta(t) = \varphi(t), \ \ \dot{\vartheta}(t_0)= \dot{\vartheta}_0, \ \ \vartheta(t_0)= \vartheta_0$

donde $\vartheta=\vartheta(t)$ es el ángulo instantáneo que forma el péndulo con la vertical.

Transformar el problema a la forma vectorial (1) ¿Cómo se resolvería utilizando el método de Euler?

Método de Heun¶

Versión 1:

Para mejorar la estimación de la pendiente se calculan dos derivadas en el intervalo (una en el punto inicial y otra al final) y se promedian.

Con el método de Euler calcular $y^0_{k+1}$ :

$y^0_{k+1} = y_k + f(x_k, y_k) h$

Calcular la estimación de la pendiente al final del intervalo:

$y'_{k+1} = f(x_{k+1},y^0_{k+1})$

Obtener la pendiente promedio en el intervalo:

$\bar{y}' = \frac{y'_k + y'_{k+1}}{2} = \frac{f(x_k, y_k) + f(x_{k+1},y^0_{k+1})}{2}$

Usar la pendiente promedio para calcular $y_{k+1}$ :

$y_{k+1} = y_k + \frac{f(x_k, y_k) + f(x_{k+1},y^0_{k+1})}{2} h$

Nota

El método de Heun es un método predictor-corrector, que tiene un solo paso y se expresa en forma concisa como:

$\begin{array}{llll} y^0_{k+1} &= &y_k + f(x_k, y_k) h \ \ & \rightarrow \text{Predictor}\\ y_{k+1} &= &y_k + \frac{f(x_k, y_k) + f(x_{k+1},y^0_{k+1})}{2} h & \rightarrow \text{Corrector}\\ \end{array}$

Versión 2:

Se predice el valor de y en el punto medio del intervalo y se calcula la derivada en ese punto:

Con el método de Euler calcular el punto medio $y_{k+\frac{1}{2}}$ :

$y_{k+\frac{1}{2}} = y_k + f(x_k, y_k) \frac{h}{2}$

Calcular la pendiente en el punto medio:

$y'_{i+\frac{1}{2}} = f(x_{k+\frac{1}{2}},y_{k+ \frac{1}{2}})$

Con la pendiente calculada, se extrapola linealmente desde $x_k$ hasta $x_{k+1}$ :

$y_{k+1} = y_k + f(x_{k+\frac{1}{2}},y_{k+ \frac{1}{2}}) h$

Métodos de Runge-Kutta¶

Los métodos de Runge-Kutta tiene la forma generalizada:

$y_{n+1} = y_n + \phi(x_n, y_n,h)h$

donde $\phi(x_n, y_n,h)$ se conoce como la función de incremento, la cual puede interpretarse como una pendiente representativa del intervalo. En forma general, $\phi(x_n, y_n,h)$ se escribe:

$\phi = a_1 k_1 + a_2 k_2 +\ldots + a_n k_n$

El método Runge-Kutta más utilizado es el de cuarto orden (RK4). Se calcula la derivada $y'=f(x,y(x))$ en 4 puntos diferentes del rectángulo de vértices $(x_n,y_n), (x_{n+1},y_n),(x_n,y_{n+1}),(x_{n+1},y_{n+1})$ , en el plano $XY$ . El esquema clásico de Runge-Kutta de cuarto orden es:

$\begin{array}{lll} k_1 &= &h f(x_n,y_n) \\ & & \\ k_2 &= &h f(x_n + \frac{h}{2},y_n + \frac{k_1}{2}) \\ & & \\ k_3 &= &h f(x_n + \frac{h}{2},y_n + \frac{k_2}{2}) \\ & & \\ k_4 &= &h f(x_n + h,y_n + k_3) \\ & & \\ y_{n+1} &= &y_n + \frac{k_1 + 2 k_2 + 2 k_3 + k_4}{6}\\ & & \\ x_{n+1} &= &x_n + h\\ \end{array}$

Gráfica RK4¶

Representación gráfica del método de Runge-Kutta de orden 4:

Ejercicio 2¶

Resolver utilizando RK4, el siguiente problema de valor inicial.

$\dfrac{dy}{dx} = 2 x y, \ \ y(1)=1, \ \ h=0.1$

Comparar el resultado con el valor exacto.

Ejercicios Propuestos¶

Programar el ejercicio 1.1 utilizando su lenguaje favorito y analizar el error.

Clase 13: Ecuaciones Diferenciales Ordinarias I¶

Introdución: Ecuaciones Diferenciales¶