Clase 14: El método del disparo¶

Bibliografía de la Clase:

Introduction to Numerical Analysis - J.Stoer, R.Bulirsch. Chapter 7: Ordinary Differential Equations.
Guía profesor Luis Salinas

EDO con condiciones de borde¶

Las ecuaciones diferenciales ordinarias con condiciones de borde aparecen al modelar problemas de la ingeniería y se caracterizan por contar con dos restricciones en los extremos del intervalo definido.

Ejemplo

Resolver la siguiente EDO con condiciones de borde:

$y' + 4y = 0 \\ y(0)=-2, \qquad y(\frac{\Pi}{4})=10$

Solución

Esta EDO tiene solución analítica y es de la forma:

$y(x) = c_1 cos(2x) + c_2 sin(2x)$

por lo tanto, lo único que falta es obtener son las constantes $c_1$ y $c_2$ determinadas por las condiciones de borde:

$y(0) = c_1 = -2 \\ y(\frac{\Pi}{4})= c_2 = 10$

La solución analítica para esta ecuación es entonces:

$y(x) = -2 cos(2x) + 10 sin(2x)$

Sin embargo, lo más común es que la función $y(x)$ no cuente con una solución analítica y se deba recurrir a métodos numéricos para estimar la función usando datos equiespaciados $x_k, k=0 \dots n$ , con $x_0=a$ y $x_n=b$ . Se cumple que $h=x_{k+1} - x_k \quad \forall k=1 \dots n-1$ .

Cuando se cuenta con la solución analítica, es posible visualizar la efectividad de los métodos numéricos.

Uno de los métodos numéricos para este tipo de problemas es el método del disparo (Shooting method).

Método del disparo para EDOs lineales¶

Una EDO lineal con condiciones de borde es de la forma:

$y'' = p(x) y' + q(x) y + r(x) \qquad a \leq x \leq b\\ y(a) = \alpha, \qquad y(b) = \beta$

El método del disparo para EDO lineales, consiste en sustuir el problema lineal con valor de frontera por dos problemas de valor inicial.

Por lo tanto se resolverán los siguientes problemas de valor inicial:

$y_1'' = p(x) y_1' + q(x) y_1 + r(x) \qquad a \leq x \leq b\\ y_1(a) = \alpha, \qquad y_1'(a) = 0$

y

$y_2'' = p(x) y_2' + q(x) y_2 + r(x) \qquad a \leq x \leq b\\ y_2(a) = 0, \qquad y_2'(a) = 1$

que pueden ser resueltos usando los métodos vistos en la Clase 13.

La solución $y(x)$ puede construirse entonces usando las soluciones $y_1(x)$ e $y_2(x)$ como:

$y(x) = y_1(x) + \frac{\beta - y_1(b)}{y_2(b)} y_2(x)$

Ejercicio en clases

Muestre que la solución anterior cumple con las condiciones de borde definidas previamente.

Método del disparo para EDOs no lineales¶

Para las EDOs no lineales, no es posible expresar la solución $y(x)$ como una combinación lineal de las soluciones de dos problemas de valor inicial, sino que se necesita un conjunto de soluciones que permitan ir convergiendo a la solución.

El método del disparo permite resolver EDOs no lineales de segundo orden de la forma:

$y'' = f(x,y,y') \qquad a \leq x \leq b \\ y(a) = \alpha, \qquad y(b) = \beta$

que consiste en resolver el problema de valor inicial:

(1) $y'' = f(x,y,y') \qquad a \leq x \leq b \\ y(a) = \alpha, \qquad y'(a) = M$

para varios valores del parámetros $M$ hasta obtener una solución $y(x)$ que satisfaga $y(b) = \beta$ .

Regula Falsi

Una forma de ir aproximándose a la solución es mediante el método Regula Falsi. Ya que se obtendrán varias funciones para distintos valores de $M$ se les denominará $y(M_k;b) \quad k=1 \dots n$ donde para algún $M_k$ se cumplirá que $y(b) = \beta$ .

Primero definamos la función:

$F(M_k) = y(M_k;b) - \beta$

notar que esta función es positiva cuando se está sobreestimando el borde $\beta$ y es negativa cuando el valor de $y(M_k;b)$ es menor que $\beta$ .

Cuando encontramos dos valores para $M$ digamos $M_1$ y $M_2$ que cumplen lo siguiente:

$F(M_1) F(M_2) < 0$

entonces podemos decir que podemos encontrar un valor $M_3$ tal que $y(M_3;b)$ que está entre $y(M_1;b)$ e $y(M_2;b)$ .

La manera de estimar $M_3$ a partir de $M_1$ y $M_2$ es usando el método de regula falsi:

$M_3=\frac{F(M_2)M_1 - F(M_1)M_2}{F(M_2)-F(M_1)}\,.$

Ejercicio propuesto

Demuestre que se cumple la expresión anterior usando el método regula falsi cuando se cumple que $F(M_1) F(M_2) < 0$ .

Método iterativo de Newton

El método iterativo de Newton es otro método para estimar un valor para $M$ tal que $y(M;b)=\beta$ . La idea es ir estimando los $M_k$ iterativamente:

(2) $M_{k+1}=M_k-\frac{y(M_k;b)-\beta}{\frac{\partial}{\partial M}y(M_k;b)}$

Para calcular $\frac{\partial}{\partial M}y(M;x)$ se introduce la variable dependiente auxiliar:

$z(x) = \frac{\partial}{\partial M} y, \qquad \text{con } \qquad y = (M;x)\,,\quad a\leq x\leq b\,,$

de modo que:

$z(b)=\frac{\partial}{\partial M} y(M;b)\,,$

que es la derivada requerida en la iteración de Newton. Ya que no se conoce una expresión explícita para $y(M;x)$ es necesario encontrar una forma de estimar $z(b)$ iterativamente.

Por simplicidad las derivadas (parciales) con respecto a 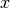$x$ se escribirán como $(\cdot)'$ .

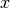Suponiendo que las derivadas parciales con respecto a $M$ y $x$ conmutan, se tiene que:

$z' &= \frac{\partial z}{\partial x} = \frac{\partial}{\partial x} \frac{\partial}{\partial M} y = \frac{\partial}{\partial M} y'\,, \\ z'' &= \frac{\partial z'}{\partial x} = \frac{\partial}{\partial x} \frac{\partial}{\partial M} y' = \frac{\partial}{\partial M} y'' = \frac{\partial}{\partial M} f\big( x,y,y'\big) \\ &= f_y\big( x,y,y' \big)\; \underset{z}{\underbrace{\frac{\partial}{\partial M} y}} + f_{y'}\big( x,y,y'\big)\; \underset{z'}{\underbrace{\frac{\partial}{\partial M} y'}} \\ &= f_y \big( x,y,y' \big)\,z + f_{y'} \big( x,y,y')\,z'$

Además se tiene que:

$z(a) =\frac{\partial}{\partial M} y(M;a) =\frac{\partial}{\partial M} \alpha = 0\,,\qquad z'(a) = \frac{\partial}{\partial M} y'(M;a) = \frac{\partial}{\partial M} M =1\,.$

Luego, la variable auxiliar $z$ satisface el siguiente problema de valor inicial:

(3) $\begin{cases} z'' &= f_y \big( x,y,y' \big)\,z + f_{y'}\big( x,y,y' \big)\,z'\,,\\ z(a)&=0\,,\qquad z'(a)=1\,. \end{cases}$

Esta ecuación se llama habitualmente ecuación variacional del problema.

Para resolver el problema se resuelven simultáneamente los problemas de valores iniciales de las ecuaciones (1) y (3) para un $M$ inicial y una malla equiespaciada de $x_j$ hasta concluir en $x=b$ . Al finalizar, se tendrá un valor para $y(M_k;b)$ y otro para $z(b) = \frac{\partial}{\partial M} y(M;b)$ que permiten calcular $M_{k+1}$ en la ecuación (2).

Clase 14: El método del disparo¶

EDO con condiciones de borde¶

Método del disparo para EDOs lineales¶

Método del disparo para EDOs no lineales¶

Contenidos

Tema anterior

Próximo tema

Esta página

Navegación

Clase 14: El método del disparo¶

EDO con condiciones de borde¶

Método del disparo para EDOs lineales¶

Método del disparo para EDOs no lineales¶

Contenidos

Tema anterior

Próximo tema

Esta página

Búsqueda rápida

Navegación