Clase 7: Algoritmos de QR iterativos¶

Bibliografía de la Clase:

Numerical Linear Algebra.L.N. Trefethen. Chapter 5: Lecture 28 QR Algorithm without Shifts
Guía profesor Luis Salinas

Equivalencia QR/Iteración Simultánea¶

Los algoritmos de Iteración simultánea y algoritmo de QR sin corrimientos son equivalentes y generan la misma secuencias de matrices. Sin embargo, el algoritmo QR es una solución más elegante y por lo tanto la más usada.

La equivalencia de estos dos algoritmos se ve reflejada en el siguiente teorema:

Teorema

Los algoritmos de Iteración simultánea y QR generan la misma secuencia de matrices $\mathbf{A}^{(k)}$ , $\underline{\mathbf{R}}^{(k)}$ y $\underline{\mathbf{Q}}^{(k)}$ que satisfacen las siguientes relaciones:

$\mathbf{A}^{k} = \underline{\mathbf{Q}}^{(k)} \underline{\mathbf{R}}^{(k)}$ .
$\mathbf{A}^{(k)}=(\underline{\mathbf{Q}}^{(k)})^T \mathbf{A} \underline{\mathbf{Q}}^{(k)}$ .

Demostración¶

Las relaciones deben demostrarse para ambos algoritmos.

Para el algoritmo de Iteración simultánea se tiene que:

$\mathbf{A}^{k} =& \mathbf{A} \mathbf{A}^{k-1} \\ =&\mathbf{A} \underline{\mathbf{Q}}^{(k-1)} \underline{\mathbf{R}}^{(k-1)} \hspace{6em} \text{inducción} \\ =& \mathbf{Z} \underline{\mathbf{R}}^{(k-1)} \hspace{9em} \text{ya que } \mathbf{Z} = \mathbf{A} \underline{\mathbf{Q}}^{(k-1)}\\ =& \underline{\mathbf{Q}}^{(k)} \mathbf{R}^{(k)} \underline{\mathbf{R}}^{(k-1)} \hspace{6em} \text{ya que } \mathbf{Z} = \underline{\mathbf{Q}}^{(k)} \mathbf{R}^{(k)} \\ =& \underline{\mathbf{Q}}^{(k)} \underline{\mathbf{R}}^{(k)} \hspace{9em} \text{ya que } \underline{\mathbf{R}}^{(k)} = \mathbf{R}^{(k)} \underline{\mathbf{R}}^{(k-1)}$

La segunda parte del teorema se cumple inmediatamente porque así está definido en el algoritmo de Iteración simultánea.

Ahora, para el algoritmo QR la primera parte del teorema se deriva como:

$\mathbf{A}^{k} =& \mathbf{A} \mathbf{A}^{k-1} \\ =&\mathbf{A} \underline{\mathbf{Q}}^{(k-1)} \underline{\mathbf{R}}^{(k-1)} \hspace{7em} \text{inducción} \\ =& \underline{\mathbf{Q}}^{(k-1)} \mathbf{A}^{(k-1)} \underline{\mathbf{R}}^{(k-1)} \hspace{5em} \text{por inducción } \mathbf{A}^{(k-1)}=(\underline{\mathbf{Q}}^{(k-1)})^T \mathbf{A} \underline{\mathbf{Q}}^{(k-1)} \\ =& \underline{\mathbf{Q}}^{(k-1)} \mathbf{Q}^{(k)} \mathbf{R}^{(k)} \underline{\mathbf{R}}^{(k-1)} \hspace{4em} \text{ya que } \mathbf{A}^{(k-1)} = \mathbf{Q}^{(k)} \mathbf{R}^{(k)}\\ =& \underline{\mathbf{Q}}^{(k)} \underline{\mathbf{R}}^{(k)} \hspace{10em} \text{ya que } \underline{\mathbf{Q}}^{(k-1)} \mathbf{Q}^{(k)} = \underline{\mathbf{Q}}^{(k)} \text{y} \mathbf{R}^{(k)} \underline{\mathbf{R}}^{(k-1)} = \underline{\mathbf{R}}^{(k)}$

Para probar la segunda parte del teorema:

$\mathbf{A}^{(k)} =& \mathbf{R}^{(k)} \mathbf{Q}^{(k)} \\ =& (\mathbf{Q}^{(k)})^T \mathbf{A}^{(k-1)} \mathbf{Q}^{(k)} \hspace{10em} \text{ya que } \mathbf{A}^{(k-1)} = \mathbf{Q}^{(k)} \mathbf{R}^{(k)} \\ =& (\mathbf{Q}^{(k)})^T (\underline{\mathbf{Q}}^{(k-1)})^T \mathbf{A} \underline{\mathbf{Q}}^{(k-1)} \mathbf{Q}^{(k)} \hspace{5em} \text{por inducción (2)} \\ =& (\underline{\mathbf{Q}}^{(k)})^T \mathbf{A} \underline{\mathbf{Q}}^{(k)} \hspace{12em} \text{ya que } \underline{\mathbf{Q}}^{(k)} = \underline{\mathbf{Q}}^{(k-1)} \mathbf{Q}^{(k)}$

Convergencia

Las dos partes de este teorema explican porqué los algoritmos converjen.

$\mathbf{A}^{k} = \underline{\mathbf{Q}}^{(k)} \underline{\mathbf{R}}^{(k)}$ muestra porqué el algoritmo espera encontrar vectores propios, ya que construye bases ortonormales para sucesivas potencias de $\mathbf{A}^k$ .
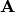$\mathbf{A}^{(k)}=(\underline{\mathbf{Q}}^{(k)})^T \mathbf{A} \underline{\mathbf{Q}}^{(k)}$ , muestra que los elementos de la diagonal de $\mathbf{A}^{(k)}$ son los cuocientes de Rayleigh de $\mathbf{A}$ correspondientes a las columnas de $\underline{\mathbf{Q}}^{(k)}$ (ejercicio en clases: demostrar). Por otra parte, los elementos fuera de la diagonal son cuocientes de Rayleigh que son aproximaciones de distintos vectores propios y que en el tiempo se vuelven ortogonales, por lo tanto convergen a 0.

Algoritmo QR con corrimientos¶

Al igual que la iteración del cuociente de Rayleigh, el algoritmo de QR converge cúbicamente. Para mejorar el rendimiento se realizan tres modificaciones al algoritmo de QR:

Preprocesamiento de la matriz $\mathbf{A}$ como matriz de Hessenberg.

Realizar el algoritmo de QR a la matriz $\mathbf{A}$ trasladada por $\mu^{(k)}\mathbb{I}$ donde $\mu^{(k)}$ son estimaciones de los valores propios. A este algoritmo se le denomina QR con corrimientos. Inicialmente se calcula la factorización QR de $\mathbf{A}^{(k)} - \mu^{(k)}\mathbb{I}$ :

$\mathbf{Q}^{(k)} \mathbf{R}^{(k)} = \mathbf{A}^{(k-1)} - \mu^{(k)}\mathbb{I}$

$\mathbf{A}^{(k)} = \mathbf{R}^{(k)} \mathbf{Q}^{(k)} + \mu^{(k)}\mathbb{I}$

Ejercicio propuesto Demostrar que $\mathbf{A}^{(k)}$ y $\mathbf{A}^{(k-1)}$ tienen los mismos valores propios.

Proceso de deflación que permite dividir la matriz $\mathbf{A}^{(k)}$ en submatrices de menor dimensión.