Clase 8: Interpolación de Newton¶
Bibliografía de la Clase:
- Guía profesor Luis Salinas
- Guía profesor Roberto León
- Introduction to Numerical Analysis - J.Stoer, R.Bulirsch
- Análisis Numérico - Richard L. Burden - J. Douglas Faires
Interpolación Polinomial¶
Las funciones polinomiales son una de las técnicas más utilizadas para ajustar una cantidad de datos y conocer su comportamiento. Este grupo de funciones son descritas como:

Es necesario especificar que 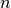 es un entero positivo, y que los
coeficientes
es un entero positivo, y que los
coeficientes  son constantes reales. El grado del polinomio es
son constantes reales. El grado del polinomio es
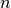 . Este tipo de funciones pueden aproximar uniformemente funciones
continuas, es decir, dada una función definida y continua en un
intervalo cerrado, existe un polinomio que es muy cercano a la
función dada.
. Este tipo de funciones pueden aproximar uniformemente funciones
continuas, es decir, dada una función definida y continua en un
intervalo cerrado, existe un polinomio que es muy cercano a la
función dada.
Definición Dada una función  y una correspondiente data
y una correspondiente data
 se llama interpolación polinomial al proceso de encontrar
un polinomio de grado menor o igual a la cantidad de datos, tal que
se llama interpolación polinomial al proceso de encontrar
un polinomio de grado menor o igual a la cantidad de datos, tal que
 , es decir, que el polinomio tome como puntos
de apoyos las abscisas de la data, y que pase por cada una de las
ordenadas.
, es decir, que el polinomio tome como puntos
de apoyos las abscisas de la data, y que pase por cada una de las
ordenadas.
Aproximación de Weierstrass¶
Este teorema afirma que las funciones reales continuas definidas en un intervalo cerrado y acotado pueden ser aproximadas tanto como se quiera por un polinomio.
Teorema:
Suponga que f está definida y es continua sobre un intervalo
[a,b]. Para cada  , existe un polinomio
, existe un polinomio  con la siguiente propiedad:
con la siguiente propiedad:
![|f(x) - p(x)| < \epsilon, \forall x \in [a,b]](_images/math/2eb9f42fd5c5f215f1805d3f4dbc563868de6422.png)
Demostración¶
La demostración de este teorema está fundamentada en la demostración
del polinomio de S. Bernstein. Consideremos ![f \in [0,1]](_images/math/1ade9be18da8e739d4e5a78394d93561d1bd8722.png) (por motivos
prácticos se define en este intervalo, ya que con el se pueden generar
otros, ya sea escalando o desplazando.
(por motivos
prácticos se define en este intervalo, ya que con el se pueden generar
otros, ya sea escalando o desplazando.

Esta sumatoria proviene del teorema del binomio:

Y además:

Diferencias Divididas¶
Sea  el polinomio interpolador en los puntos
el polinomio interpolador en los puntos  (grado máximo k).
(grado máximo k).

Considerando los polinomios  y su diferencia:
y su diferencia:

vemos que para los puntos  tenemos que:
tenemos que:

y también que para el siguiente punto  tenemos que
tenemos que  , sin conocerse el valor a priori de lo que pueda dar
, sin conocerse el valor a priori de lo que pueda dar
 . Por lo tanto, el polinomio
. Por lo tanto, el polinomio  verifica:
verifica:

Por otro lado,  es un polinomio de grado máximo
es un polinomio de grado máximo 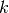 ya que es
la resta de dos polinomios,
ya que es
la resta de dos polinomios,  de grado
de grado 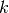 y
y  de
grado
de
grado  y según se acaba de ver se anula en los k puntos
anteriores. Entonces, el término que no se “pierde” es
y según se acaba de ver se anula en los k puntos
anteriores. Entonces, el término que no se “pierde” es  y además
y además
 tiene como raices, los
tiene como raices, los  , por lo
que se puede expresar
, por lo
que se puede expresar  de la siguiente forma:
de la siguiente forma:

Para el punto  se cumple que:
se cumple que:

y despejando  de la última expresión, se tiene:
de la última expresión, se tiene:

Gracias a estas expresiones se introduce el concepto de diferencias divididas:
Definición:
Dada la función  de la cual se conoce su valor en los puntos
de la cual se conoce su valor en los puntos  , se llama diferencia dividida de
, se llama diferencia dividida de  en los puntos
en los puntos
 al valor
al valor ![f[x_0,x_1,\ldots,x_k]](_images/math/0fc05294b043a6d80cbc1a31d8f0abc22caa742e.png) y se calcula recursivamente como:
y se calcula recursivamente como:
![f[x_i] = f(x_i) = y_i](_images/math/7a0de47ca32e4b48a3c4d7d9ef74f805a265a363.png)
![f[x_i, x_{i+1}] = \frac{f[x_{i+1}]-f[x_i]}{x_{i+1}-x_i}](_images/math/0d2f5138aae19e959182b438a779ffe90b59973a.png)
![f[x_i, x_{i+1}, \ldots, x_{i+k}] = \frac{f[x_{i+1}, x_{i+2},\ldots,x_{i+k}] - f[x_{i}, x_{i+1},\ldots,x_{i+k-1}]}{x_{i+k}-x_i}](_images/math/f79df9d648f51acbe5128913ca79081f413861fa.png)
El cuadro esquemático de las diferencias divididas es:
![\begin{array}{lllll}
x_0 \rightarrow & y_0 = f[x_0] \searrow & & & \\
& & f[x_0,x_1] \searrow & & \\
x_1 \rightarrow & y_1 = f[x_1] \nearrow & & f[x_0,x_1,x_2] \searrow & \\
& & f[x_1,x_2] \nearrow & & f[x_0,x_1,x_2,x_3] \\
x_2 \rightarrow & y_2 = f[x_2] & & f[x_1,x_2,x_3] \nearrow & \\
& & f[x_2,x_3] & & \\
x_3 \rightarrow & y_3 = f[x_3] & & & \\
\end{array}](_images/math/f53f424a8b8ba8c7ab3c2ad3a715161d9770f9c4.png)
Los números obtenidos en la parte superior corresponden a los coeficientes del polinomio interpolador. En general:
![a_k = f[x_0,x_1,\dots,x_k]](_images/math/03149a9bda76c0a5a7c330daa51381e90c69f3c0.png)
El polinomio interpolador para la figura corresponde a:
![p(x) &= f[x_0] + f[x_0, x_1](x-x_0) + \\
&f[x_0,x_1,x_2](x-x_0)(x-x_1) + \\
&f[x_0,x_1,x_2,x_3](x-x_0)(x-x_1)(x-x_3)](_images/math/c5b9eb0ff9b94a80d232ef278bca903ff27eb51d.png)


![\begin{array}{c c c c c}
\hline
x & y & f[x_i,x_i+1] & f[x_i, x_{i+1}, x_{i+2}] & f[x_i, \ldots, x_{i+3}] \\
\hline
0 & \textbf{-1} & & & \\
& & \textbf{1} & & \\
1 & 0 & & \textbf{3} & \\
& & 7 & & \textbf{1} \\
2 & 7 & & 7 & \\
& & 28 & & \\
4 & 63 & & & \\
\hline
\end{array}](_images/math/1ed9fed5a2b2c9c99a7c76bff26d84c982e5ee4a.png)

