Contenidos
Tema anterior
Próximo tema
Clase 11: Más sobre Factorización QR
Esta página
Búsqueda rápida
Enter search terms or a module, class or function name.
- Numerical Linear Algebra.L.N. Trefethen. Chapter 1: Lecture 7 QR Factorization
- Introduction to Linear Algebra. Gilbert Strang. Chapter 4, Sec. 4.4 Orthogonal Bases and Gram-Schmidt
- Guía profesor Luis Salinas
Recordar:
Propiedades de la Ortogonalidad:
Preserva la estructura geométrica en el espacio Euclideano se preserva el producto interno:
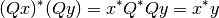
Por lo tanto, el tamaño de los vectores se preserva:
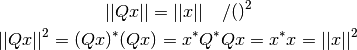
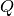 aplica una transformación a
aplica una transformación a  , que no afecta al tamaño del vector.
, que no afecta al tamaño del vector.
Gram-Schmidt
El método de Gram-Schimdt permite realizar la ortogonalización de vectores.

1. Para construir el vector 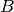 , ortogonal al vector
, ortogonal al vector  (a partir del vector
(a partir del vector 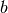 )
se debe quitar al vector b su proyección sobre a, es decir:
)
se debe quitar al vector b su proyección sobre a, es decir:
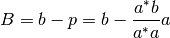
Importante:
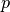 es un vector que corresponde a la proyección del vector
es un vector que corresponde a la proyección del vector 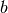 sobre el vector
sobre el vector  :
: 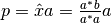 .
.
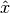 es un escalar y se obtiene de la siguiente manera:
es un escalar y se obtiene de la siguiente manera:
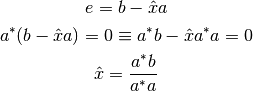
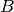 es ortogonal con el vector
es ortogonal con el vector  .
.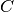 ortogonal a
ortogonal a 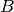 y
y 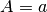 .
.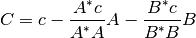
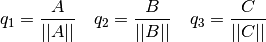
Por lo tanto, la idea de Gram-Schmidt es restar de cada nuevo vector, sus proyecciones de los vectores ya ortonormalizados.
Ejercicio en clases:
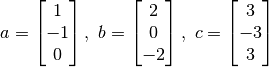
Nota:
Si 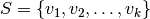 es un conjunto de vectores no nulos, ortogonales de a pares, entonces
es un conjunto de vectores no nulos, ortogonales de a pares, entonces 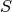 es linealmente independiente (l.i.). Pero esta implicancia no es hacia el otro lado, i.e., si son l.i, no son necesariamente ortogonales.
es linealmente independiente (l.i.). Pero esta implicancia no es hacia el otro lado, i.e., si son l.i, no son necesariamente ortogonales.
Sean
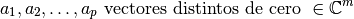
Los espacios generados por estos vectores se denotan:
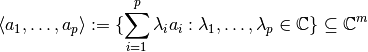
A menudo nos interesa los espacios de columnas (sucesivos) genereado por las columnas de  :
:
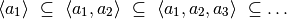
La idea de la factorización QR es la construcción de una secuencia ortonormal
de vectores 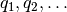 que genera estos subespacios sucesivos.
que genera estos subespacios sucesivos.
Sea 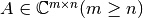 de full rank
de full rank 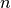 . Se busca la secuencia
. Se busca la secuencia 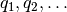 con la propiedad:
con la propiedad:
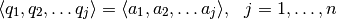
lo que corresponde a:
![\left[ \begin{array}{c|c|c|c}
\, & \, & \, & \, \\
\, & \, & \, & \, \\
a_1 & a_2 & \cdots & a_n \\
\, & \, & \, & \, \\
\, & \, & \, & \,
\end{array} \right]=
\left[ \begin{array}{c|c|c|c}
\, & \, & \, & \, \\
\, & \, & \, & \, \\
q_1 & q_2 & \cdots & q_n \\
\, & \, & \, & \, \\
\, & \, & \, & \,
\end{array} \right]
\begin{bmatrix}
r_{11} & r_{12} & \ldots & r_{1n} \\
\, & r_{22} & \, & \, \\
\, & \, & \ddots & \, \\
\, & \, & \, & r_{nn}
\end{bmatrix}](_images/math/8ddad0bdc1f240581dfc7ecc0586219baf8af654.png)
como ecuaciones queda:
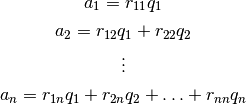
matricialmente:
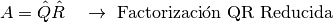
y gráficamente:

donde 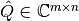 con columnas ortonormales y
con columnas ortonormales y
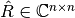 , triangular superior.
, triangular superior.
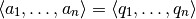
las columnas 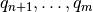 deben ser ortogonales al
deben ser ortogonales al 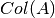 .
.
Si  es de full rank
es de full rank 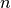 , estos vectores forman una base ortonormal de
, estos vectores forman una base ortonormal de
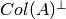 (espacio ortogonal al
(espacio ortogonal al 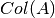 , que corresponde al
, que corresponde al 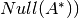 .
.

Ya se sabe cual es la idea de la ortogonalización de Gram-Schmidt, más formalmente:
Gram-Scmidt Clásico:
En la iteración j-ésima, encontrar el vector 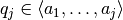 que sea ortogonal a
que sea ortogonal a 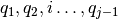 :
:
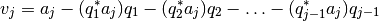
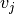 corresponde al tipo de vector requerido, pero todavía no está
normalizado, por lo que simplemente
corresponde al tipo de vector requerido, pero todavía no está
normalizado, por lo que simplemente 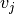 debe ser dividido por su norma,
debe ser dividido por su norma,
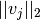 .
.
Por lo tanto:
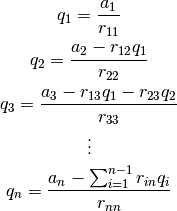
donde
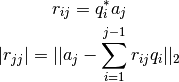
A continuación, el algoritmo de Gram-Schmidt Clásico, el cual númericamente no es muy estable debido a errores de redondeo (que analizaremos en las siguientes clases):

Ejercicio en clases:
Obtener factorización QR para 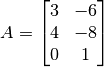 .
.