Contenidos
Tema anterior
Próximo tema
Esta página
Búsqueda rápida
Enter search terms or a module, class or function name.
Bibliografía de la Clase:
Cuando resolvemos el sistema 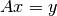 el efecto que produce
el efecto que produce  sobre el vector
sobre el vector  puede explicarse usando la descomposición SVD
puede explicarse usando la descomposición SVD 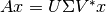 . La siguiente figura explica gráficamente lo que sucede:
. La siguiente figura explica gráficamente lo que sucede:

 ¶
¶Teorema
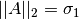 y
y 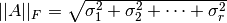
Demostración
Las dos demostraciones se basan en que tanto la norma 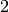 como la de Frobenius son invariantes ante la multiplicación de matrices unitarias.
como la de Frobenius son invariantes ante la multiplicación de matrices unitarias.
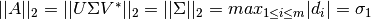
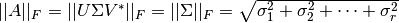
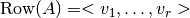 donde
donde 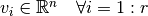
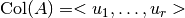 donde
donde 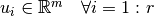
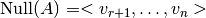 donde
donde 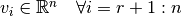
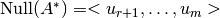 donde
donde 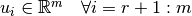
Lo anterior se resume en la siguiente imagen:

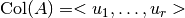 .
.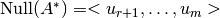 .
.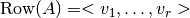 .
.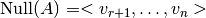 .
.La descomposición de valores propios la expresamos matricialmente como:
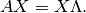
Por otro lado, la descomposición de valores singulares (SVD) se expresa como:
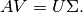
Las principales diferencias entre ambas descomposiciones son:
 tiene una SVD.
tiene una SVD.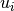 y
y 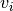 ) son ortonormales, los vectores
) son ortonormales, los vectores 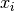 no son necesariamente ortogonales.
no son necesariamente ortogonales.Nota
Los vectores 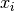 de una matriz simétrica son ortogonales.
de una matriz simétrica son ortogonales.
La compresión de imágenes es una importante aplicación en álgebra lineal debido a la necesidad de minimizar la cantidad de información almacenada y transmitida. SVD es una técnica que permite minimizar el espacio requerido para almacenar una imagen conservando la calidad de ella.
Si tenemos una imagen de 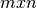 pixeles la podemos representar matricialmente con su respectiva SVD:
pixeles la podemos representar matricialmente con su respectiva SVD:
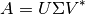
Equivalentemente podemos expresar la imagen representada en  como:
como:
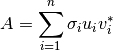
Debido a que 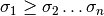 los términos de mayor impacto son los primeros términos de la expresión anterior.
los términos de mayor impacto son los primeros términos de la expresión anterior.
Por lo tanto, es posible aproximar la imagen  usando sólo los primeros
usando sólo los primeros 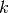 términos de la serie.
términos de la serie.
Inicialmente la memoria requerida para almacenar una imagen era 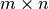 . Usando la SVD sólo se requiere de
. Usando la SVD sólo se requiere de 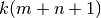 , es decir, el crecimiento es lineal.
, es decir, el crecimiento es lineal.
Para asegurar que la memoria usada no supere la original debe cumplirse:
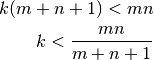
Un ejemplo de esta compresión se muestra en el siguiente código en Matlab: