Contenidos
Tema anterior
Próximo tema
Esta página
Búsqueda rápida
Enter search terms or a module, class or function name.
- Numerical Linear Algebra.L.N. Trefethen. Chapter 1: Lecture 7 QR Factorization
- Introduction to Linear Algebra. Gilbert Strang. Chapter 4, Sec. 4.4 Orthogonal Bases and Gram-Schmidt
- Guía profesor Luis Salinas
Teorema Existencia:
Toda matriz 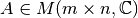 con
con 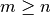 tiene factorización QR completa, por lo tanto también tiene factorización QR reducida.
tiene factorización QR completa, por lo tanto también tiene factorización QR reducida.
Demostración
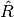 y
y 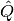 .
.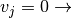 no se puede normalizar para producir
no se puede normalizar para producir 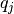
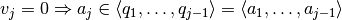 y esto significa que
y esto significa que  no tiene full rank, lo que ¡es una contradicción!.
no tiene full rank, lo que ¡es una contradicción!.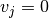 , y en ese momento se toma cualquier
, y en ese momento se toma cualquier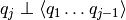 con
con 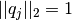 y luego se
y luego seTeorema Unicidad
Toda matriz 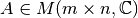 con
con 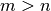 de full rank tiene una factorización única
de full rank tiene una factorización única 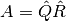 con
con 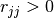 .
.
Los vectores se convierten en funciones continuas:
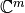 pasamos al espacio
pasamos al espacio ![L^{2}[-1,1]](_images/math/0fbfd0250d4152e3c080362b9fa053ad1f6b3df4.png) (¡por ejemplo!) con producto interno.
(¡por ejemplo!) con producto interno.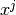 :
:![(f,g):= \int_{-1}^{1}\bar{f}(x)g(x)dx, \ \ \ f,g \in L^{2}[-1,1]
\left[ \begin{array}{c|c|c|c}
\, & \, & \, & \, \\
\, & \, & \, & \, \\
1 & x^{1} & \cdots & x^{n-1} \\
\, & \, & \, & \, \\
\, & \, & \, & \,
\end{array} \right]](_images/math/d57da2bf66bf32c039ee7c840f5858674a544398.png)
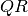 toma la forma:
toma la forma:![A=QR= \left[ \begin{array}{c|c|c|c}
\, & \, & \, & \, \\
\, & \, & \, & \, \\
q_0(x) & q_1(x) & \cdots & q_{n-1}(x) \\
\, & \, & \, & \, \\
\, & \, & \, & \,
\end{array} \right]
\begin{bmatrix}
r_{0,0} & r_{0,1} & \ldots & r_{0,n-1} \\
\, & r_{1,1} & \, & \, \\
\, & \, & \ddots & \, \\
\, & \, & \, & r_{n-1,n-1}
\end{bmatrix}](_images/math/357ebb2bc3431bd4cfd201ec468abb61bdddf756.png)
donde:
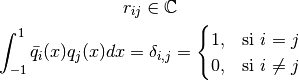
Para obtener 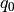 :
:
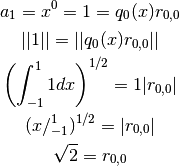
Tarea: Obtener 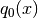 y
y 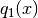 .
.