Contenidos
Tema anterior
Clase 11: Más sobre Factorización QR
Próximo tema
Clase 13: Ortogonalización de Gram-Schmidt
Esta página
Búsqueda rápida
Enter search terms or a module, class or function name.
Bibliografía de la Clase:
La proyección de un vector en un espacio vectorial puede ser vista como la sombra del vector en el espacio. Cuando proyectamos un vector en el espacio generado por otro vector (una recta) se puede ver como la siguiente imagen:
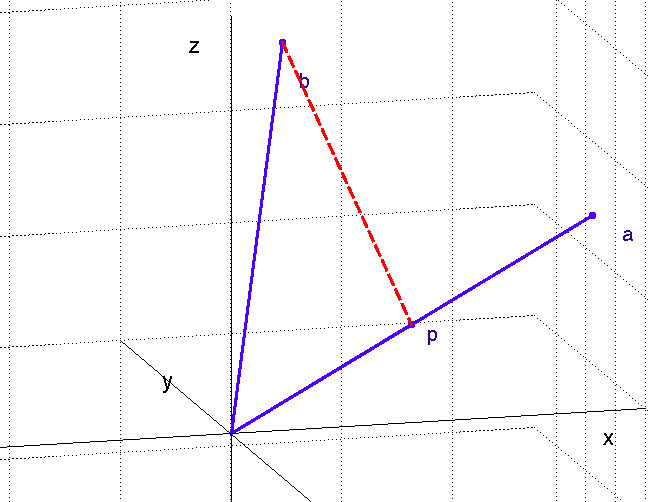
donde se proyecta el vector 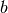 ortogonalmente en el espacio generado por el vector
ortogonalmente en el espacio generado por el vector  generando el vector
generando el vector 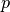 .
.
La matriz que permite encontrar 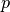 se le denomina matriz de proyección
se le denomina matriz de proyección 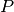 , por lo tanto se cumple que:
, por lo tanto se cumple que:
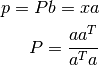
donde 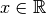 .
.
Demostración
Dado que 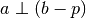 se tiene que:
se tiene que:
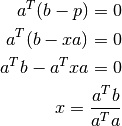
lo que nos permite expresar 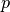 como:
como:
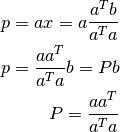
En la siguiente imagen se muestra la proyección de un vector en un plano:

Análogamente, la matriz de proyección en un plano, o en general en un espacio vectorial
generado por las columnas de una matriz 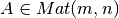 es:
es:
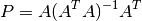
Demostración
Sean 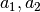 vectores bases del plano mostrado en la figura y la matriz:
vectores bases del plano mostrado en la figura y la matriz:
![A=\left[ \begin{array}{c|c}
\, & \, \\
a_1 & a_2 \\
\, & \,
\end{array} \right]`](_images/math/1a91adfcb99e2fc508a47d2afa8f4a9e6a5dc992.png)
donde el vector 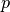 vive en el plano (
vive en el plano (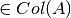 ), por lo tanto puede ser expresado como
), por lo tanto puede ser expresado como
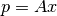 para algún
para algún 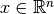 (en este caso
(en este caso 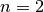 ).
Se observa que el vector
).
Se observa que el vector 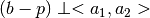 y se tiene lo siguiente:
y se tiene lo siguiente:
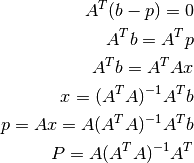
Nota
Proyectores ortogonales no son matrices ortogonales.
Propiedades
Un proyector es una matriz cuadrada 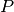 que satisface
que satisface 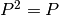 . Adicionalmente, los proyectores ortogonales cumplen que
. Adicionalmente, los proyectores ortogonales cumplen que 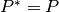 .
.
Si 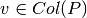 podemos reescribir
podemos reescribir 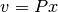 para algún
para algún  . La proyección de
. La proyección de  sería:
sería:
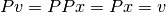
En este caso se tiene que:
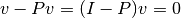
es decir 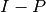 proyecta el
proyecta el 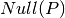 . Se dice que
. Se dice que 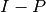 es el proyector complementario de
es el proyector complementario de 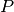 .
.
Por otro lado si 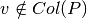 significa que
significa que 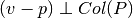 , por lo tanto:
, por lo tanto:
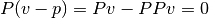
es decir que 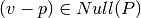 .
.
Para todo proyector se tiene:
Espacios
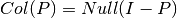
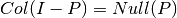
Si definimos 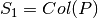 y
y 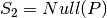 se dice que
se dice que 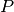 proyecta sobre
proyecta sobre 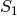 a lo largo de
a lo largo de 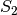 .
.
Sea 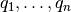 una base para
una base para 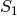 y
y 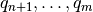 una base para
una base para 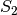 el proyector puede escribirse como:
el proyector puede escribirse como:
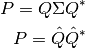
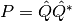 . Ayuda:
. Ayuda: 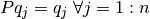 .
.Considere las bases ![b_1=[2 \; 1]^T](_images/math/c9197ef9a5271a8f82d6b0e11fd080cc2e5736ca.png) y
y ![b_2=[3 \; 7]^T](_images/math/4b3357b69d48a0feea1e29b4899ec5fd1c27c397.png) . Determinar el proyector sobre el espacio generado por
. Determinar el proyector sobre el espacio generado por 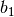 a lo largo del espacio generado por
a lo largo del espacio generado por 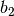 .
.