Bibliografía de la Clase:
La factorización QR nos permite descomponer A como:
![\left[ \begin{array}{c|c|c|c}
\, & \, & \, & \, \\
\, & \, & \, & \, \\
a_1 & a_2 & \cdots & a_n \\
\, & \, & \, & \, \\
\, & \, & \, & \,
\end{array} \right]=
\left[ \begin{array}{c|c|c|c}
\, & \, & \, & \, \\
\, & \, & \, & \, \\
q_1 & q_2 & \cdots & q_n \\
\, & \, & \, & \, \\
\, & \, & \, & \,
\end{array} \right]
\begin{bmatrix}
r_{11} & r_{12} & \ldots & r_{1n} \\
\, & r_{22} & \, & \, \\
\, & \, & \ddots & \, \\
\, & \, & \, & r_{nn}
\end{bmatrix}](_images/math/8ddad0bdc1f240581dfc7ecc0586219baf8af654.png)
Análogamente, podemos ver que cada columna de 
puede expresarse como combinación lineal de las columnas de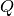 
de la siguiente manera:
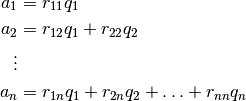
El algoritmo clásico que permite encontrar esta descomposición es el siguiente:
en el cual, en cada iteración se realiza la siguiente operación sobre los vectores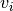 
:
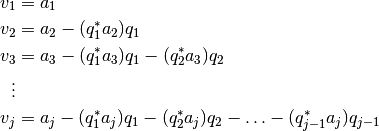
La expresión anterior puede reescribirse como:
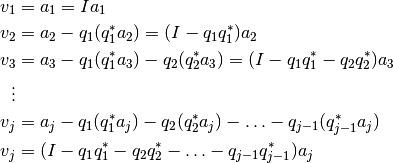
donde la matriz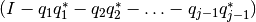 
corresponde al proyector ortogonal complementario a los vectores 
.
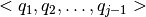Si definimos
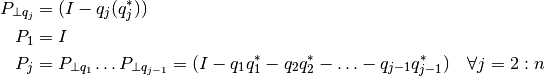
podemos reescribir los vectores como:
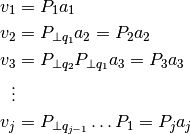
En base al enfoque basado en proyectores anterior, podemos ver que es posible aplicar la proyección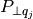 
a todos los vectores: 
.
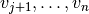El algoritmo siguiente muestra este enfoque:
