Contenidos
Tema anterior
Clase 14: Triangularización de Householder
Próximo tema
Clase 16: Más de Mínimos Cuadrados
Esta página
Búsqueda rápida
Enter search terms or a module, class or function name.
Bibliografía de la Clase
- Numerical Linear Algebra. L.N. Trefethen. Chapter 2, Lecture 11: Least Squares Problems
- Guía profesor Luis Salinas
Contexto:
En algebra lineal, el problema corresponde a solucionar un sistema sobredeterminado de ecuaciones 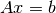 (no cuadrado) con más filas que columnas.
(no cuadrado) con más filas que columnas.
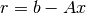 .
.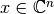 tal que
tal que 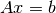 , donde
, donde 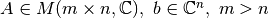 .
.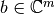 y
y 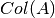 tiene dimensión, a lo más
tiene dimensión, a lo más 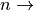 se dice que el sistema está sobredeterminado.
se dice que el sistema está sobredeterminado.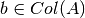 .
.Idea
Resto = 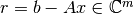
Se desea obtener un  lo más pequeño posible.
lo más pequeño posible.
pequeño
tamaño
norma
Por lo tanto el problema toma la siguiente forma:
Dado, encontrar un
tal que
sea mínima.
Geométricamente: Encontrar un vector 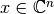 tal que
tal que 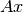 “sea cercano” a
“sea cercano” a 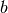 .
.
Se comparará la interpolación polinomial de datos, que corresponde a un sistema de ecuaciones cuadrado, con el ajuste polinomial de mediante mínimos cuadrados, el cual es un sistema rectangular.
Interpolación polinomial: Dado un conjunto de datos encontrar un polinomio que pasa exactamente por esos datos 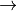 sistema de ecuaciones cuadrado.
sistema de ecuaciones cuadrado.
Si se tienen 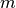 puntos distintos
puntos distintos 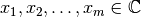 y datos
y datos  , para esos puntos se debe encontrar un polinomio tal que:
, para esos puntos se debe encontrar un polinomio tal que:
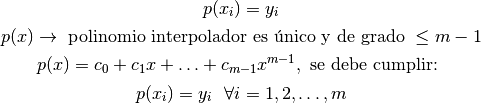
La relación de 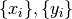 con los coeficientes
con los coeficientes 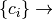 Matriz de Vandermode.
Matriz de Vandermode.

Sistema de ecuaciones cuadrado:
![\begin{bmatrix} 1 &x_{1} &x^{2}_{1} &\ldots &x^{m-1}_{1} \\ 1 &x_{2} &x^{2}_{2} &\ldots &x^{m-1}_{2} \\ \ldots &\ldots &\ldots &\ldots &\vdots \\ & & & \\ 1 &x_{m} &x^{2}_{m} &\ldots &x^{m-1}_{m} \end{bmatrix}
\begin{bmatrix} c_0 \\ c_1 \\ \vdots \\ c_{m-1}\end{bmatrix}=
\begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_m \end{bmatrix}
\text{O en forma más compacta: }
[x_{i}^{j}][c_{i}]=[y_{i}], \ \ 1 \leq i \leq m, \ \ 0\leq j \leq m-1](_images/math/f38281b71f9a13ab02ce20009157263d3a54c5f3.png)
Tiene solución si: ![det[x_{i}^{j}] \neq 0](_images/math/8d094eac71d02899fd8c2fcb8d65a5a4c61c142c.png) . Este sistema si tiene solución, pero el ajuste es malo en los bordes, y el problema está mal condicionado, ya que es muy sensibles a pequeñas perturbaciones en los datos.
. Este sistema si tiene solución, pero el ajuste es malo en los bordes, y el problema está mal condicionado, ya que es muy sensibles a pequeñas perturbaciones en los datos.

La figura anterior corresponde a una interpolación mediante un polinomio de grado 10 que ajusta 11 datos.
Ejercicio:
Se tienen los siguientes datos:
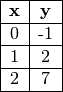
La interpolación polinomial produce oscilaciones en los bordes y es muy sensible a las perturbaciones en los datos, por lo tanto, para evitar esto se debe reducir el grado del polinomio.
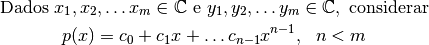
Si 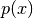 minimiza
minimiza 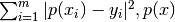 corresponde al ajuste de datos por mínimos cuadrados.
corresponde al ajuste de datos por mínimos cuadrados.
Considerando los datos del ejercicio anterior, la siguiente figura muestra la curva obtenida mediante interpolación polinomial (azul) y mediante mínimos cuadrados (curva verde):

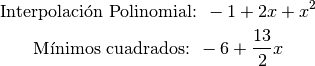
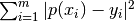 es el cuadrado de la norma del resto
es el cuadrado de la norma del resto 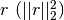 para el sistema rectangular:
para el sistema rectangular:![\begin{bmatrix} 1 &x_{1} &x^{2}_{1} &\ldots &x^{n-1}_{1} \\ 1 &x_{2} &x^{2}_{2} &\ldots &x^{n-1}_{2} \\ \ldots &\ldots &\ldots &\ldots &\vdots \\ & & & \\ 1 &x_{m} &x^{2}_{m} &\ldots &x^{n-1}_{m} \end{bmatrix} \begin{bmatrix}c_{0} \\ c_{1} \\ \vdots \\ c_{n-1}\end{bmatrix} \approx \begin{bmatrix} y_{1} \\ y_{2} \\ \vdots \\ y_{m}\end{bmatrix}
\text{ O en forma más compacta:}
[x_{i}^{j}] \ [c_{j}] \approx [y_{i}] \ \ 1 \leq i \leq m \ \ \ 0 \leq \ j \leq n-1](_images/math/4610140b7203b14b33b4d66e9eb7d398afcf84b3.png)
Ejemplo:

Objetivo:
Encontrar el punto 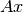 más cercano a
más cercano a 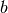 , en el
, en el 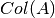 , por lo tanto,
, por lo tanto, 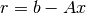 se minimiza.
se minimiza.

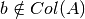 , el sistema de ecuaciones
, el sistema de ecuaciones 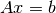 no tiene solución
no tiene solución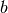 sobre el
sobre el 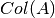
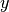 está dado por la proyección ortogonal de
está dado por la proyección ortogonal de 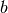 en el
en el 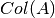
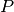 que transforma
que transforma 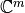 al
al 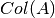
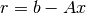 debe ser ortogonal al
debe ser ortogonal al 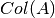
Teorema:
Sea 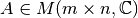 y
y 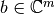 . El vector
. El vector 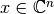 minimiza
minimiza 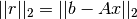
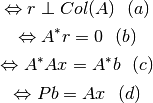
donde 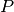 es el proyector ortogonal sobre
es el proyector ortogonal sobre 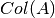 .
.
El sistema de ecuaciones de 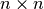 de (c) es conocido como ecuaciones normales, y es no singular ssi
de (c) es conocido como ecuaciones normales, y es no singular ssi  es full rank
es full rank 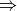 la solución de
la solución de  es única ssi
es única ssi  tiene full rank.
tiene full rank.
Sea 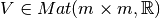 , la matriz de Vandermonde. Demostrar que
, la matriz de Vandermonde. Demostrar que 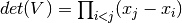 .
.