Contenidos
- Clase 2: Espacios Vectoriales y Multiplicación de Matrices
Tema anterior
Próximo tema
Clase 3: Transformaciones lineales y subespacios fundamentales
Esta página
Búsqueda rápida
Enter search terms or a module, class or function name.
Desde el punto de vista físico, un vector es una cantidad con magnitud y dirección:
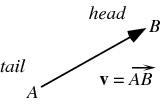
Desde el punto de vista matemático un vector se define formalmente como un elemento del espacio vectorial [Wolfram]. En el espacio vectorial 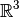 (espacio Euclideano de dimensión 3), sus elementos corresponden a vectores tridimensionales de la forma:
(espacio Euclideano de dimensión 3), sus elementos corresponden a vectores tridimensionales de la forma:
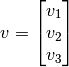
Ahora es importante definir formalmente un espacio vectorial:
Un espacio vectoriales un conjunto que es cerrado bajo la suma de vectores y la multiplicación escalar. Para un espacio vectorial en general, los escalares son miembros de un campo
(
, por lo tanto
se denomina espacio vectorial sobre
Por lo tanto, un espacio vectorial debe cumplir con:
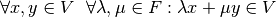
Ejemplo 1: Espacio vectorial 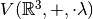 , donde cada elemento del espacio es representado como un tupla de 3 números de
, donde cada elemento del espacio es representado como un tupla de 3 números de 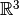 .
.
Ejemplo 2: 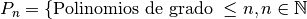 }:
}:
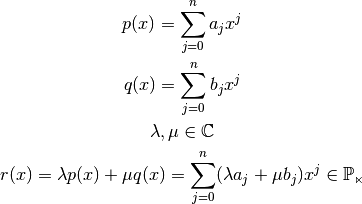
Por lo tanto, 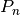 es un espacio vectorial con escalares en
es un espacio vectorial con escalares en 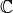 .
.
Los vectores, elementos del espacio vectorial, se pueden sumar (y restar) y multiplicar por escalares. Combinando ambas operaciones se obtienen las combinaciones lineales.
Definición: Sean 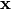 y
y 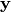 dos vectores del espacio vectorial
dos vectores del espacio vectorial 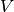 , la suma
de
, la suma
de 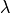
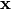 y
y 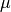
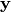 es la combinación lineal de
es la combinación lineal de 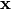 y
y 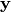 .
.
Hay 4 cuatro combinaciones lineales importanes:
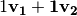
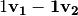
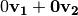
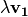 en la dirección de
en la dirección de 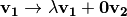
Los vectores 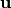 ,
, 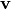 son linealmente dependientes (l.d.) ssi
son linealmente dependientes (l.d.) ssi 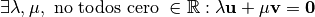 . Esto es equivalente a:
. Esto es equivalente a:
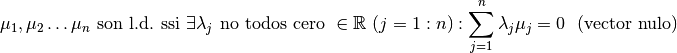
En la expresión precedente, es importante el término 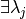 , el
cual implica que no todos los
, el
cual implica que no todos los 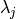 son 0, es decir, existen números
son 0, es decir, existen números
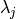 que permiten que un vector pueda ser expresado como la suma de
otros vectores.
que permiten que un vector pueda ser expresado como la suma de
otros vectores.
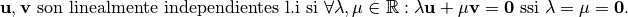
La idea es que un vector no se pueda expresar mediante la suma de otros vectores.
Responder:
Si 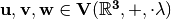 :
:
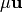 ?
?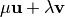 ?
?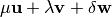 ?
?La transformación 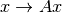 (
( matriz de
matriz de 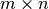 ), es lineal si
para cualquier
), es lineal si
para cualquier 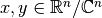 y cualquier
y cualquier 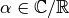 se cumple:
se cumple:
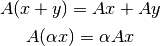
Se puede pensar en dos enfoques para resolver el clásico problema de 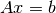 (que será un tema de análisis en nuestro curso): enfoque fila y enfoque
columna. Si tomamos el ejemplo propuesto en [StrangVL]:
(que será un tema de análisis en nuestro curso): enfoque fila y enfoque
columna. Si tomamos el ejemplo propuesto en [StrangVL]:
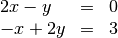

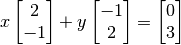
Ejercicio en clase
Ahora pasemos a 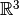 :
:
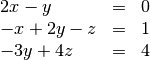
Enfoque Fila:
Generar matrices 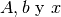
2.1 Geométricamente, ¿qué representa cada fila?
2.2 Geométricamente, ¿qué se obtiene con la intersección de “dos filas”?
2.3 Geométricamente, ¿qué se obtiene con la intersección de “tres filas”?
Enfoque Columna
Multiplicar Ax=b:
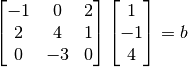
Considerar la matriz 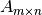 y el vector n-dimensional
y el vector n-dimensional  :
:
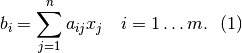
Sea 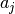 la j-ésima columna de
la j-ésima columna de  , vector de dimensión
, vector de dimensión 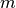 , se puede reescribir (1):
, se puede reescribir (1):
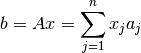
Multiplicar nuevamente Ax=b usando este enfoque, ¿qué se obtiene?
¡Esto corresponde a las combinaciones lineales de los vectores columnas de la
matriz A! 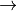 Es importante para entender los algoritmos que se verán en la clase
Es importante para entender los algoritmos que se verán en la clase
Sea 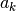 la k-ésima columna de la matriz
la k-ésima columna de la matriz  :
:
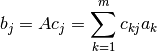
Esto corresponde a las combinaciones lineales de los vectores columnas de la
matriz A, 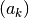 , con los coeficientes
, con los coeficientes 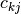 !!.
!!.
Sea 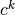 la k-ésima fila de la matriz
la k-ésima fila de la matriz 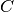 :
:
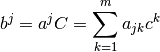
Esto corresponde a las combinaciones lineales de los vectores filas de la
matriz C, 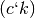 , con los coeficientes
, con los coeficientes 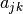 !!.
!!.
Tarea (exposición opcional próxima clase), explicar la multiplicación de matrices enfoque columna fila
| [Wolfram] | Vector. Wolfram MathWorld. http://mathworld.wolfram.com/Vector.html |
| [StrangVL] | MIT OpenCourseWare (OCW). Linear Algebra, Gilbert Strang. Video Lectures. http://ocw.mit.edu/courses/mathematics/18-06-linear-algebra-spring-2010/video-lectures/ |