Contenidos
Tema anterior
Clase 2: Espacios Vectoriales y Multiplicación de Matrices
Próximo tema
Clase 4: Vectores ortogonales y matrices
Esta página
Búsqueda rápida
Enter search terms or a module, class or function name.
Bibliografía de la Clase:
Sean 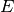 y
y 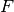 espacios vectoriales sobre un cuerpo
espacios vectoriales sobre un cuerpo 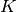 , de dimensiones
, de dimensiones 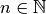 y
y 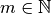 respectivamente.
Sean
respectivamente.
Sean 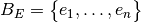 y
y 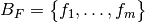 bases de
bases de 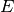 y
y 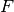 , respectivamente.
Entonces, los vectores
, respectivamente.
Entonces, los vectores 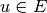 y
y 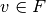 se escriben de manera única en términos de las respectivas bases.
Utilizaremos la siguiente notación estándar:
se escriben de manera única en términos de las respectivas bases.
Utilizaremos la siguiente notación estándar:
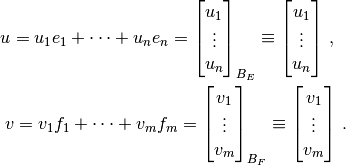
Se dice entonces que los 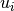 y los
y los 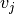 son las coordenadas de los vectores
son las coordenadas de los vectores 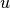 y
y  relativas a las bases
relativas a las bases
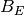 y
y 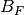 , respectivamente.
, respectivamente.
Sea 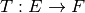 una transformación u operador lineal.
Entonces se tiene:
una transformación u operador lineal.
Entonces se tiene:
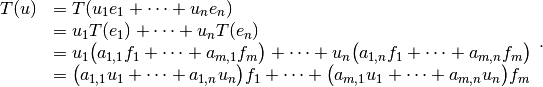
En particular se tiene:
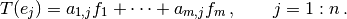
La expresión anterior puede escribirse de la siguiente forma matricial:

La matriz ![A=\big[ a_{ij}\big]_{m\times n}](_images/math/6be1cb372fe791aa4c0b5e08431f8527e37ffaae.png) se
denomina matriz de la transformación lineal
se
denomina matriz de la transformación lineal 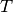 relativa a las
bases
relativa a las
bases 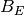 y
y 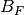 . Nótese que los coeficientes
. Nótese que los coeficientes 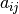 ,
, 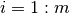 corresponden a los coeficientes de la
corresponden a los coeficientes de la 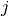 -‘esima
columna de
-‘esima
columna de  .
.
De manera más compacta se acostumbra a escribir:
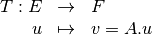
Ejercicio:
Dado los vectores base del espacio vectorial V: 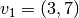 y
y 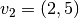 y los vectores base del espacio vectorial W:
y los vectores base del espacio vectorial W: 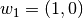 y
y 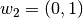 encuentre la matriz de la transformación lineal
encuentre la matriz de la transformación lineal 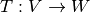 y
y 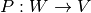 .
.
Ya sabemos que los espacios vectoriales deben cumplir con las siguientes condiciones:
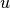 ,
, 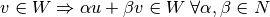
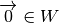
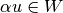
Un subespacio de un espacio vectorial es el espacio vectorial generado por un conjunto 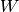 de vectores, donde
de vectores, donde 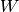 sea un subconjunto de los vectores que generan el espacio vectorial
sea un subconjunto de los vectores que generan el espacio vectorial 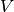 . El subespacio, por lo tanto, debe cumplir con todas las propiedades de los espacios vectoriales.
. El subespacio, por lo tanto, debe cumplir con todas las propiedades de los espacios vectoriales.
Ejemplo: Dos vectores en 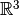 generan un plano en
generan un plano en 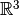 . El plano constituye un subespacio vectorial de
. El plano constituye un subespacio vectorial de 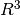 .
.
Se define como el 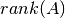 como la dimensión de su espacio de columnas.
Equivalentemente se define como el número de vectores columna independientes.
Una forma de determinar el
como la dimensión de su espacio de columnas.
Equivalentemente se define como el número de vectores columna independientes.
Una forma de determinar el 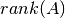 es calculando el número de pivotes que resultan
del método de Eliminación de Gauss-Jordan.
es calculando el número de pivotes que resultan
del método de Eliminación de Gauss-Jordan.
Una matriz 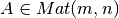 es full rank si
es full rank si 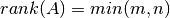 .
.
Ejercicio:
Determine el rank de la siguiente matriz:
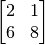
Nota
Una matriz cuadrara se dice no singular o invertible si es full rank.
A partir de la matriz  es posible distinguir cuatro subespacios fundamentales:
es posible distinguir cuatro subespacios fundamentales:

Los cuatro subespacios fundamentales son los siguientes:
1) Espacio de columnas
A todas las posibles combinaciones lineales de las columnas de A
se le denomina el espacio de columnas de A, conocido también como
el 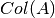 o
o 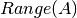 .
.
Sea 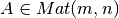 . Se sabe que
. Se sabe que 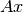 representa una combinación lineal de las columnas de
representa una combinación lineal de las columnas de  . Por lo tanto,
cualquier vector
. Por lo tanto,
cualquier vector 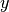 en el espacio generado por las columnas de
en el espacio generado por las columnas de  puede escribirse como:
puede escribirse como:
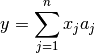
Es decir,
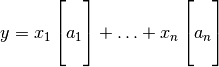
Ejercicio Describir el espacio de columnas para las siguientes matrices:
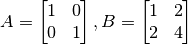
2) Espacio Nulo
Espacio generado por todas las soluciones  de
de 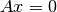 . A este
espacio se conoce como Nullspace
. A este
espacio se conoce como Nullspace 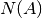 .
.
Para algunas matrices, la única solución para resolver 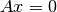 es
es 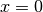 .
En este caso en
.
En este caso en 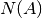 es el vector nulo.
es el vector nulo.
3) Espacio de filas
Espacio generado por todas las posibles combinaciones de las filas de A,
conocido también como 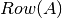 .
.
El espacio de filas es equivalente a encontrar el 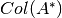 .
.
4) Espacio Nulo izquierdo
Espacio generado por todas las soluciones  de
de 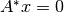 . A este
espacio se conoce como left Nullspace
. A este
espacio se conoce como left Nullspace 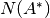 .
.
Ejercicio Opcional:
Sea 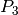 el espacio vectorial de los polinomios reales de
grado a lo más 3, equipado con su base canónica
el espacio vectorial de los polinomios reales de
grado a lo más 3, equipado con su base canónica 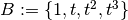 .
.
Sea 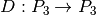 el operador diferencial definido
por:
el operador diferencial definido
por:
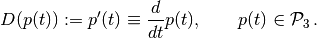
Encuentre la matriz del operador D.