Contenidos
Tema anterior
Clase 3: Transformaciones lineales y subespacios fundamentales
Próximo tema
Esta página
Búsqueda rápida
Enter search terms or a module, class or function name.
Bibliografía de la Clase:
Matriz Conjugada o Adjunta
Se llama matriz conjugada o adjunta de una matriz 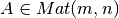 a la matriz
a la matriz 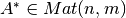 definida como
definida como 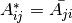 . Si
. Si  es una matriz de coeficientes reales,
es una matriz de coeficientes reales, 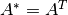 donde
donde 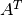 es la matriz traspuesta de
es la matriz traspuesta de  .
.
Donde 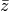 es el complejo conjugado de un escalar
es el complejo conjugado de un escalar  . Si
. Si 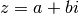 , entonces
, entonces 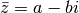 .
.
Matriz hermitiana
Se dice que  es hermitiana si
es hermitiana si 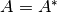 . Si
. Si  es real y
es real y 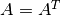 se dice también que
se dice también que  es una matriz simétrica.
es una matriz simétrica.
Por ejemplo,
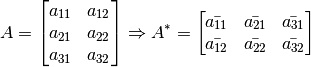
Dos propiedades importantes de las matrices son:
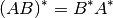
Por otro lado,
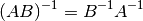
Producto Interno
El producto interno es la generalización del producto punto (definido para coeficientes reales). Sean dos vectores 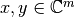 su producto interno se define como:
su producto interno se define como: 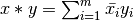 .
.
La norma euclideana del vector  puede ser definida en términos del producto interno como:
puede ser definida en términos del producto interno como:
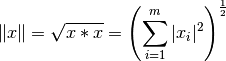
De manera equivalente, el producto interno se define en términos del ángulo que forman los vectores:

En la figura puede verse que el ángulo entre los vectores 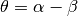 . Por lo tanto se tiene:
. Por lo tanto se tiene:
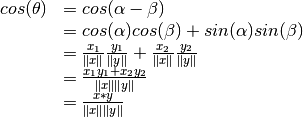
El producto interno sirve también para representar la proyección (o sombra) de un vector sobre otro. En la siguiente imagen se muestra la proyección del vector  sobre
sobre 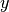 .
.

Puede verse que la proyección o sombra del vector  sobre
sobre 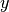 denotado como
denotado como 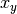 corresponde a:
corresponde a:
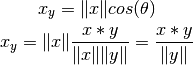
Asi mismo puede definirse la proyección de 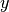 sobre
sobre  como
como 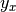 :
:
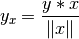
Definición
Dos vectores 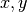 son ortogonales si
son ortogonales si 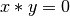 . Es decir, si no se proyectan uno en el otro.
. Es decir, si no se proyectan uno en el otro.
Se dice que un conjunto de vectores en 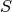 es ortogonal si
es ortogonal si 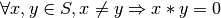 . Este conjunto
. Este conjunto 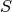 se dirá además ortonormal si es ortogonal y además
se dirá además ortonormal si es ortogonal y además 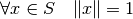 .
.
Se tiene un conjunto de vectores ortonormales 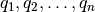 y
y  un vector arbitrario. Ya sabemos que la proyección de
un vector arbitrario. Ya sabemos que la proyección de  en el vector
en el vector 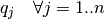 es la siguiente:
es la siguiente:
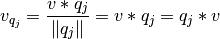
Entonces  puede expresarse como:
puede expresarse como:
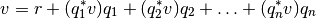
Que corresponde al vector descompuesto en 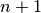 componentes ortogonales:
componentes ortogonales:
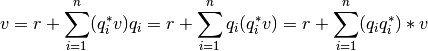
Definición
Una matriz cuadrada 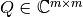 es unitaria (si es real decimos ortogonal) si
es unitaria (si es real decimos ortogonal) si 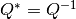 , i.e si
, i.e si 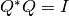 .
.
![\begin{bmatrix}
\quad & q_1^* & \quad \\ \hline
\quad & q_2^* & \quad \\ \hline
\quad & \vdots & \quad \\ \hline
\quad & q_m^* & \quad \\
\end{bmatrix} \left[ \begin{array}{c|c|c|c}
\, & \, & \, & \, \\
q_1 & q_2 & \cdots & q_m \\
\, & \, & \, & \,
\end{array} \right] = \begin{bmatrix} 1 & \, & \, & \, \\
\, & 1 & \, & \, \\
\, & \, & \ddots & \, \\
\, & \, & \, & 1
\end{bmatrix}](_images/math/5a754e582b2dece1cc2ee762c496bdf32af50306.png)
Ejercicio Opcional
Dada la matriz ![A = [I \quad I]](_images/math/f39ce67a74a22a5b8917bd3ce830871f0253f3a5.png) escribir cualquier vector
escribir cualquier vector  como una combinación de las bases del espacio de filas y del espacio nulo.
como una combinación de las bases del espacio de filas y del espacio nulo.