Contenidos
Tema anterior
Clase 4: Vectores ortogonales y matrices
Próximo tema
Esta página
Búsqueda rápida
Enter search terms or a module, class or function name.
Consideremos el espacio vectorial 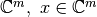 . La norma de vectores es la función función:
. La norma de vectores es la función función:
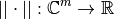
que asigna un valor real a cada vector  , y ese valor, corresponde a la longitud
del vector.
, y ese valor, corresponde a la longitud
del vector.
Una norma, 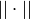 , debe cumplir las siguientes propiedades:
, debe cumplir las siguientes propiedades:
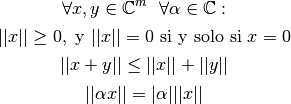
Una matriz de 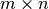 puede ser vista como un vector de dimension
puede ser vista como un vector de dimension 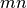 ,
y cada una de la
,
y cada una de la 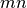 entradas de la matrix sería vista como una coordenada
independiente. Por lo tanto, cada una de las normas vistas anteriormente
podrían ser usadas para “medir el tamaño” de la matriz.
entradas de la matrix sería vista como una coordenada
independiente. Por lo tanto, cada una de las normas vistas anteriormente
podrían ser usadas para “medir el tamaño” de la matriz.
Pero cuando se trabaja con espacios de matrices, mejor usar normas asociadas a las matrices, y así aparecen las normas de matrices inducidas , o también denominadas normas naturales.
Norma Inducida o Norma Natural
(Notación del libro de Trefethen)
Sea 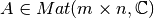 , y
, y 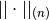 y
y 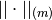 , normas de vectores en
, normas de vectores en 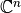 y
y 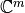 , respectivamente, la norma inducida o norma natural,
, respectivamente, la norma inducida o norma natural, 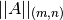 , es el menor número
, es el menor número 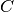 que satisface la siguiente desigualdad para todo
que satisface la siguiente desigualdad para todo 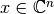 :
:
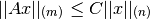
En otras palabras, 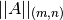 es el supremum de la proporción
es el supremum de la proporción
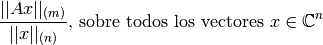
lo que implica que es el máximo factor en que la matriz  puede "estirar"
cualquier vector
puede "estirar"
cualquier vector  .
.
Se dice que 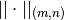 es la norma matricial inducida por las
normas (de vectores)
es la norma matricial inducida por las
normas (de vectores) 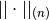 y
y 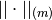 .
.
Considerar:
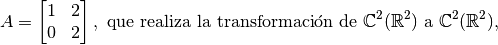
y los vectores 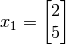 y
y 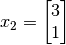 , ambos en
, ambos en 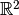 .
.
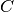 considerando la p-norma,
considerando la p-norma, 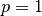 .
.Norma natural (version 2)
Debido a que el factor de estiramiento es independiente del tamaño de los vectores que se están estirando, es conveniente (y equivalente) definir la norma inducida en términos de vectores unitarios (norma igual a 1):
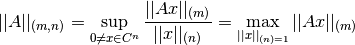
Consideremos nuevamente:
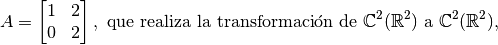
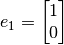 y
y 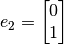 ?
? , aplicada a las esferas unitarias de 1-norma, 2-norma e
, aplicada a las esferas unitarias de 1-norma, 2-norma e 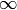 -norma.
-norma.Si 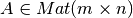 ,
, 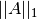 es el “máximo de las sumas de las
columnas” de A. Si se consideran los vectores columans,
es el “máximo de las sumas de las
columnas” de A. Si se consideran los vectores columans, 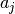 de la matriz
de la matriz  ,
los cuales son vectores m-dimensionales.
,
los cuales son vectores m-dimensionales.
La esfera unitaria de 1-norma, corresponde a 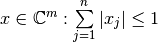 .
.
Cualquier vector 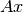 satisface:
satisface:
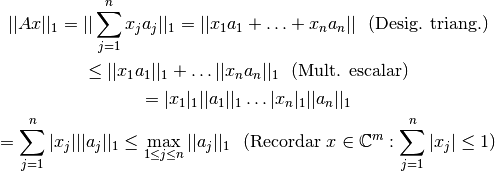
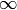 -norma de una Matriz¶
-norma de una Matriz¶Utilizando el mismo argumento anterior, se puede demostrar que la
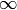 -norma de una matriz de
-norma de una matriz de 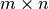 es igual a “el máximo de la suma
de las filas”:
es igual a “el máximo de la suma
de las filas”:
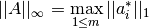
donde 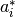 corresponde a la i-ésima fila de A.
corresponde a la i-ésima fila de A.
La norma de Frobenius o norma 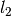 de la matriz
de la matriz  considerada como un vector en
considerada como un vector en 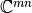 :
:
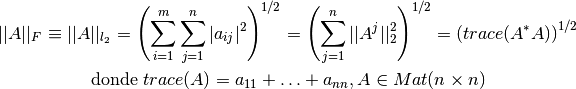
También se le conoce como norma de Schur o norma de Hilbert-Schmidt.
| [p-norms] | Imagen obtenida de Wikipedia. http://en.wikipedia.org/wiki/File:Vector_norms2.svg |