Contenidos
Tema anterior
Próximo tema
Clase 7: Valores y vectores propios
Esta página
Búsqueda rápida
Enter search terms or a module, class or function name.
Calcular p-normas, con 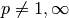 resulta más complicado, y para abordar
este problema se puede usar la propiedad de que los productos internos pueden
ser acotados usando p-normas.
resulta más complicado, y para abordar
este problema se puede usar la propiedad de que los productos internos pueden
ser acotados usando p-normas.
Sea 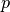 y
y 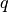 , tal que
, tal que 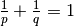 , con
, con 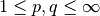 . La desigualdad de Hölder establece que para todo
. La desigualdad de Hölder establece que para todo  e
e 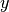 :
:
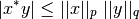
La desigualdad de Cauchy-Schwarz es el caso especial para 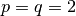
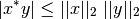
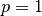 y
y 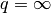 ¶
¶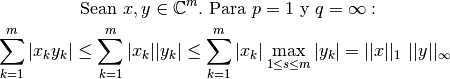
La demostración general para 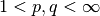 se encuentra en la guía de
ejercicios del Prof. Luis Salinas.
se encuentra en la guía de
ejercicios del Prof. Luis Salinas.
Considerar la matriz  que contiene solo una fila. La matriz puede escribirse como
que contiene solo una fila. La matriz puede escribirse como 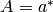 , siendo
, siendo  un vector columna.
un vector columna.
La Desigualdad de Cauchy-Schwarz permite obtener la norma inducida de una matriz, para 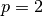 .
.
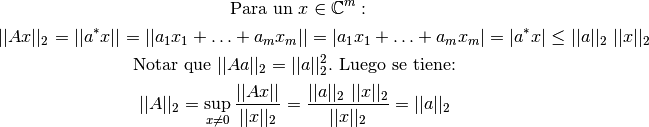
En la clase anterior se definieron las propiedades de una norma vectorial. Las nnormas matriciales, deben satisfacer las tres propiedades de una norma vectorial, y ademas una cuarta propiedad:
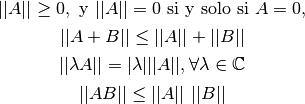
La norma de Frobenius puede ser usada para acotar el producto de matrices.
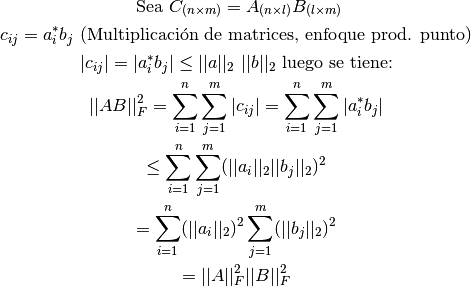
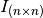 la matriz identidad, calcule la norma de
la matriz identidad, calcule la norma de 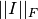 (norma de Frobenius) e
(norma de Frobenius) e 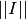 (norma inducida considerando la p-norma, con
(norma inducida considerando la p-norma, con 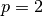 , en
, en 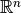 y
y 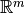 ). Hint: Las normas son distintas.
). Hint: Las normas son distintas.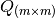 una matriz unitaria. Demostrar que
una matriz unitaria. Demostrar que 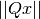 preserva la norma del vector
preserva la norma del vector 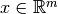 , es decir, la transformación que aplica
, es decir, la transformación que aplica 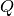 al vector
al vector  , no modifica su tamaño.
, no modifica su tamaño.