Clase 7: Valores y vectores propios¶

Bibliografía de la Clase:

Numerical Linear Algebra.L.N. Trefethen. Chapter 5: Lecture 24 Eigenvalue Problems
Introduction to Linear Algebra. Gilbert Strang. Chapter 6 Eigenvalues and Eigenvectors
Guía profesor Luis Salinas

Visualización de vectores y valores propios¶

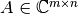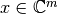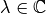Sea $A \in \mathbb{C}^{m \times n}$ . Un vector no negativo $x \in \mathbb{C}^m$ es un vector propio de $A$ y $\lambda \in \mathbb{C}$ su valor propio correspondiente si se cumple:

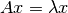
$Ax = \lambda x$

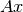En otras palabras, existen ciertos vectores $x$ para los cuales $A x$ sólo modifica su norma.

Descomposición de valores propios¶

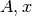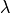La descomposición de valores propios viene dada como la generalización de la relación entre $A,x$ y $\lambda$ . Se tiene:

$\begin{bmatrix} \quad & \quad & \quad\\ \quad & A & \quad\\ \quad & \quad & \quad \end{bmatrix} \left[ \begin{array}{c|c|c|c} \, & \, & \, & \, \\ x_1 & x_2 & \cdots & x_m \\ \, & \, & \, & \, \end{array} \right]= \left[ \begin{array}{c|c|c|c} \, & \, & \, & \, \\ x_1 & x_2 & \cdots & x_m \\ \, & \, & \, & \, \end{array} \right] \begin{bmatrix} \lambda_1 & \, & \, & \, \\ \, & \lambda_2 & \, & \, \\ \, & \, & \ddots & \, \\ \, & \, & \, & \lambda_m \end{bmatrix}$

En una notación más resumida:

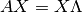
$A X = X \Lambda$

Polinomio característico¶

Para determinar los vectores propios usamos la siguiente ecuación:

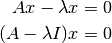
$Ax-\lambda x=0 \\ (A-\lambda I) x=0$

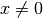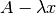Nos interesa encontrar un $x \neq 0$ (solución no trivial) del sistema. Por lo tanto, la matriz $A - \lambda x$ es una matriz singular. Toda matriz singular tiene determinante nulo. Dado esto se tiene:

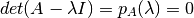
$det(A-\lambda I) = p_A(\lambda) = 0$

Por el teorema fundamental del álgebra se puede escribir el polinomio característico como:

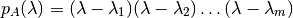
$p_A(\lambda)=(\lambda - \lambda_1)(\lambda - \lambda_2) \dots (\lambda - \lambda_m)$

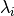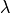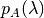Donde algunos $\lambda_i$ podrían aparecer más de una vez. Se define la multiplicidad de un valor propio $\lambda$ como su multiplicidad en el polinomio $p_A(\lambda)$ .

Nota

Aunque la matriz sea real, algunos de sus valores propios pueden ser complejos.

Diagonalización de una matriz¶

Matriz diagonalizable

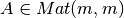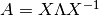Un matriz $A \in Mat(m,m)$ es diagonalizable si puede escribirse como $A=X \Lambda X^{-1}$ .

Teorema

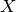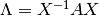Si $X$ es no singular, entonces $A$ y $\Lambda=X^{-1} A X$ tienen el mismo polinomio característico y valores propios.

Demostración

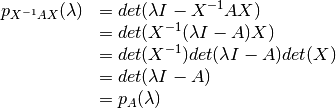
$\begin{array}{rl} p_{X^{-1}A X}(\lambda)&= det(\lambda I - X^{-1}A X)\\ &= det(X^{-1}(\lambda I -A)X) \\ &= det(X^{-1}) det(\lambda I -A) det(X) \\ &= det(\lambda I -A)\\ &= p_A(\lambda) \end{array}$

Diagonalización Unitaria¶

En el caso de que los valores propios sean elegidos ortogonales y unitarios la diagonalización de la matriz $A$ puede escribirse como:

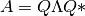
$A=Q \Lambda Q*$

Ejercicios:

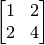
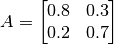
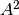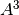Encontrar los valores y vectores propios de la siguiente matriz:

$\begin{bmatrix} 1 & 2\\ 2 & 4 \end{bmatrix}$

Diagonalizar la matriz:

$A=\begin{bmatrix} 0.8 & 0.3 \\ 0.2 & 0.7 \\ \end{bmatrix}$

Encontrar valores y vectores propios de $A^2$ , $A^3$ y $A^{10}$ .

Determinante y la traza¶

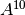Teorema

EL determinante y la traza de $A$ son iguales al producto y la suma respectivamente de lo valores propios de A.

Demostración

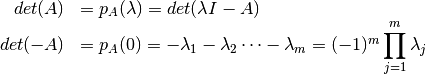
$\begin{array}{rl} det(A)&=p_A(\lambda)=det(\lambda I - A)\\ det(-A)&=p_A(0)=-\lambda_1 - \lambda_2 \dots -\lambda_m = (-1)^m \displaystyle\prod_{j=1}^m\lambda_j \end{array}$

Por las propiedades del determinante se sabe que:

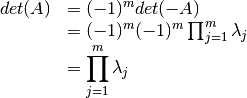
$\begin{array}{rl} det(A)&=(-1)^m det(-A)\\ &=(-1)^m (-1)^m \prod_{j=1}^m\lambda_j\\ &=\displaystyle\prod_{j=1}^m\lambda_j \end{array}$

Ejercicio propuesto¶

Demostrar que:

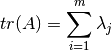
$tr(A)=\sum_{i=1}^m \lambda_j$

Usando el concepto de diagonalización de matrices demuestre lo siguiente:

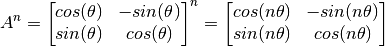
$A^n=\begin{bmatrix} cos(\theta) & -sin(\theta) \\ sin(\theta) & cos(\theta) \end{bmatrix}^n= \begin{bmatrix} cos(n \theta) & -sin(n \theta) \\ sin(n \theta) & cos(n \theta) \end{bmatrix}$

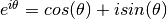Pruebe que los vectores propios de $A$ son: $\begin{bmatrix}1 \\ i \end{bmatrix}$ y $\begin{bmatrix} i \\ 1 \end{bmatrix}$ . (Ayuda: usar fórmula de Euler $e^{i\theta}=cos(\theta) + i sin(\theta)$ ).

Contenidos

Tema anterior

Próximo tema

Esta página

Clase 7: Valores y vectores propios¶

Visualización de vectores y valores propios¶

Descomposición de valores propios¶

Polinomio característico¶

Diagonalización de una matriz¶

Diagonalización Unitaria¶

Determinante y la traza¶

Ejercicio propuesto¶

Navegación

Contenidos

Tema anterior

Próximo tema

Esta página

Búsqueda rápida

Clase 7: Valores y vectores propios¶

Visualización de vectores y valores propios¶

Descomposición de valores propios¶

Polinomio característico¶

Diagonalización de una matriz¶

Diagonalización Unitaria¶

Determinante y la traza¶

Ejercicio propuesto¶

Navegación