Contenidos
Tema anterior
Clase 7: Valores y vectores propios
Próximo tema
Esta página
Búsqueda rápida
Enter search terms or a module, class or function name.
Bibliografía de la Clase:
En la siguiente figura se muestra el efecto de multiplicar la matriz  por los vectores unitarios (círculo verde).
En particular
por los vectores unitarios (círculo verde).
En particular 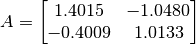 .
.

Hay ciertos vectores  que el efecto de ser multiplicados por
que el efecto de ser multiplicados por  resultan ser los semiejes de la elipse de la figura.
Tanto los vectores
resultan ser los semiejes de la elipse de la figura.
Tanto los vectores  y
y  son unitarios y los coeficientes
son unitarios y los coeficientes 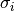 corresponden a los largos de los semiejes.
Por lo tanto, podemos resumir la imagen en las siguientes ecuaciones:
corresponden a los largos de los semiejes.
Por lo tanto, podemos resumir la imagen en las siguientes ecuaciones:
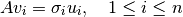
Si la matriz 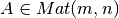 y
y 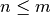 entonces se encontrarán a lo más
entonces se encontrarán a lo más 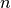 valores de
valores de 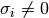 y por lo tanto la ecuación anterior sigue siendo válida aún si
y por lo tanto la ecuación anterior sigue siendo válida aún si  no es cuadrada.
La representación matricial correspondiente sería:
no es cuadrada.
La representación matricial correspondiente sería:
![\begin{bmatrix}
\quad & \quad & \quad\\
\quad & \quad & \quad\\
\quad & A & \quad \\
\quad & \quad & \quad \\
\quad & \quad & \quad
\end{bmatrix}
\left[ \begin{array}{c|c|c|c}
\, & \, & \, & \, \\
\, & \, & \, & \, \\
v_1 & v_2 & \cdots & v_n \\
\, & \, & \, & \, \\
\, & \, & \, & \,
\end{array} \right]=
\left[ \begin{array}{c|c|c|c}
\, & \, & \, & \, \\
\, & \, & \, & \, \\
u_1 & u_2 & \cdots & u_n \\
\, & \, & \, & \, \\
\, & \, & \, & \,
\end{array} \right]
\begin{bmatrix}
\sigma_1 & \, & \, & \, \\
\, & \sigma_2 & \, & \, \\
\, & \, & \ddots & \, \\
\, & \, & \, & \sigma_n
\end{bmatrix}](_images/math/8f203c4a42a62c17312069c124b6985e09244c6e.png)
De manera más resumida la expresión anterior se puede escribir como:
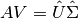
A esta factorización se denomina SVD reducida. Donde 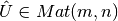 es una matriz con
es una matriz con 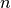 columnas ortonormales y
columnas ortonormales y 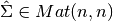 es una matriz diagonal donde
es una matriz diagonal donde 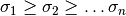 .
Dado que
.
Dado que  es una matriz unitaria (i.e
es una matriz unitaria (i.e 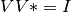 ) podemos reescribir la expresión anterior como:
) podemos reescribir la expresión anterior como:
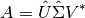
Bajo esta representación, los vectores de la matriz 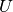 se les denomina los vectores singulares izquierdos de
se les denomina los vectores singulares izquierdos de  y a los vectores de
y a los vectores de 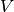 los vectores singulares derechos de
los vectores singulares derechos de  .
.
Gráficamente la factorización SVD reducida se visualiza como sigue:

La versión completa de la SVD se obtiene extendiendo la matriz 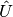 a una matriz unitaria
a una matriz unitaria 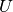 .
Gráficamente la factorización SVD completa:
.
Gráficamente la factorización SVD completa:

Al aumentar las columnas de U, también debemos extender 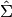 obteniendo la matriz
obteniendo la matriz 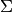 .
Para obtener
.
Para obtener 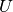 se agregaron
se agregaron 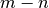 columnas ortonormales (si
columnas ortonormales (si  es full rank) o
es full rank) o 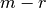 (si
(si  es el rango de la matriz
es el rango de la matriz  ).
En el caso de que
).
En el caso de que  no es full rank, deben también agregarse
no es full rank, deben también agregarse 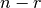 columnas a V.
columnas a V.
Las matrices 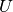 ,
, 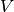 y
y 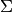 pueden ser obtenidas mediante el siguiente procedimiento:
pueden ser obtenidas mediante el siguiente procedimiento:
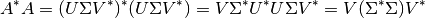
Donde 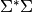 corresponde a la matriz diagonal:
corresponde a la matriz diagonal:
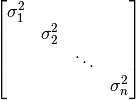
Es decir, los vectores propios de 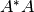 son los vectores singulares derechos de
son los vectores singulares derechos de  ,i.e
,i.e 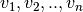 y los valores propios de
y los valores propios de 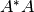 corresponden a los cuadrados de los valores singulares (
corresponden a los cuadrados de los valores singulares (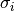 ) de
) de  .
.
Una vez obtenidas las matrices  y
y 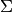 el cálculo de U es directo.
el cálculo de U es directo.
Encontrar la descomposición SVD de la siguiente matriz:
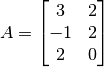
 .
. .
. .
.Considerando la proyección de vectores vistas en la clase 4. Es posible obtener un vector ortogonal a un conjunto de vectores ortonormales 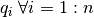 como:
como:
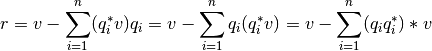
Este procedimiento (conocido como ortogonalización de Gram-Schmidt) puede ser usado para agregar vectores ortonormales a la matriz  para que encontrar la matriz unitaria
para que encontrar la matriz unitaria  .
.
Utilizando esta información, obtenga la descomposición SVD completa de  .
.